 of
of 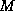 samples obtained from
the samples of the received signal.
The key to MUSIC is its data model
samples obtained from
the samples of the received signal.
The key to MUSIC is its data model
MUSIC detects frequencies in a signal by performing an eigen decomposition
on the covariance matrix of a data vector  of
of 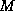 samples obtained from
the samples of the received signal.
The key to MUSIC is its data model
samples obtained from
the samples of the received signal.
The key to MUSIC is its data model

where  is a vector of
is a vector of 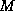 noise samples,
noise samples,  is a vector
of
is a vector
of 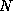 signal amplitudes (
signal amplitudes (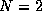 for DTMF tones), and
for DTMF tones), and
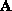 is the
is the 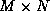 Vandermonde matrix of samples of the signal
frequencies.
If we assume a zero-mean signal and white noise, then
the covariance of
Vandermonde matrix of samples of the signal
frequencies.
If we assume a zero-mean signal and white noise, then
the covariance of  has the form
has the form
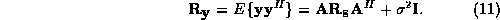
Here, 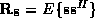 is the
is the  signal autocorrelation matrix,
signal autocorrelation matrix,  is the
is the 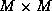 identity matrix, and
identity matrix, and 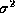 is the noise variance.
From the eigen decomposition of
is the noise variance.
From the eigen decomposition of 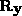 , we use the eigenvectors
associated with the
, we use the eigenvectors
associated with the 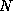 maximum eigenvalues to define the signal subspace
(the column space of
maximum eigenvalues to define the signal subspace
(the column space of 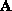 ), and use the other eigenvectors to define
the noise subspace,
), and use the other eigenvectors to define
the noise subspace, 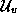 .
From the orthogonality of the signal and noise subspaces, finding the
peaks in the estimator function
.
From the orthogonality of the signal and noise subspaces, finding the
peaks in the estimator function
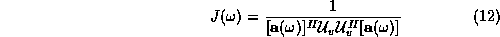
for various  values yields the strongest frequencies [1],
where
values yields the strongest frequencies [1],
where 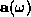 refers to the columns of
refers to the columns of 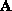 .
.
MUSIC assumes that the number of samples 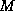 and the number of frequencies
and the number of frequencies
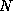 are known.
The efficiency of MUSIC is the ratio of the theoretical smallest
variance, given by the Cramer-Rao Lower Bound (CRLB) [11],
to the variance of the MUSIC estimator:
are known.
The efficiency of MUSIC is the ratio of the theoretical smallest
variance, given by the Cramer-Rao Lower Bound (CRLB) [11],
to the variance of the MUSIC estimator:

The efficiency does not depend on the total number of samples, 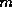 ,
(Figure 1) but does depend on
,
(Figure 1) but does depend on 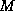 (Figure 2).
As
(Figure 2).
As 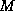 increases, efficiency and computation time increase.
We pick
increases, efficiency and computation time increase.
We pick 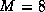 , because larger values do not significantly improve
the efficiency.
, because larger values do not significantly improve
the efficiency.