Edwin Ng
Supervisor : Professor Richard Newton
In this report, a new methodology of doing PCB routing is presented. This new methodology allows 45 degrees and multi-layer routing. More importantly the method guarantees to find the solution, if one exists, in much less time compared to other routers like the maze router. It proceeds in two phases:

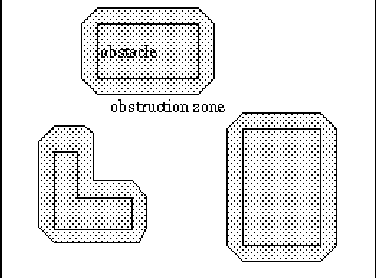
Figure 1 Typical obstacles in our PCB routing model
By using the scan line algorithm, we can dissect the free routing area into trapezoids (Figure 2). The run-time complexity of the operation is proven to be O(nlogn). While the horizontal and vertical scanning may produce different results, there are claims that such asymmetry won't impair the quality of the result. We will verify this claim after we have implemented the prototype. For now, we will just use one of the scanning orientation.
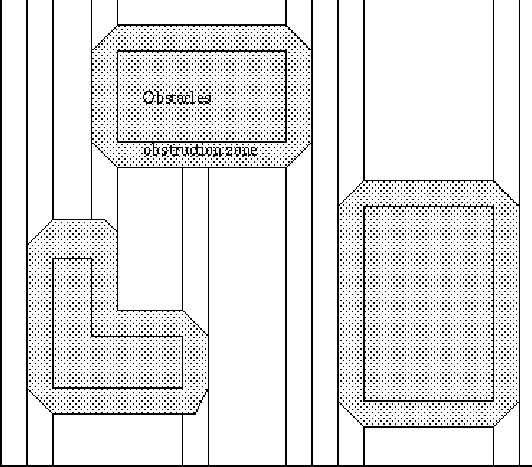
Figure 2 : Routing area after dissection
While the trapezoidal dissection approach is intuitively attractive, it nonetheless complicates the global routing phase significantly, since we have almost three times more trapezoids to deal with as compared to the case where we can approximate the corners by octhogonal lines and thus dividing the regions into rectangles instead (Figure 3). This will be one of the experiments we will try out in our prototype implementation. Three dissection strategies will be implemented :
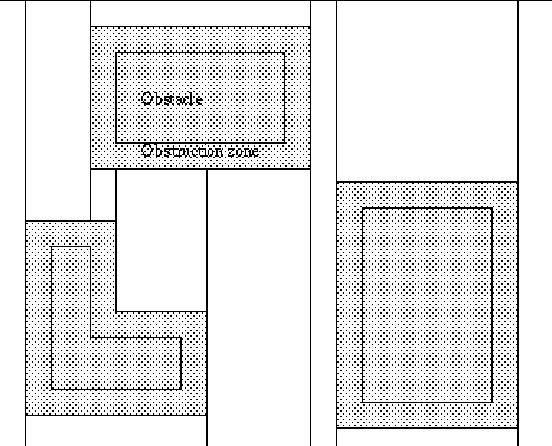
Figure 3 : Regional dissection based on rectangular obstacles
Each edge in the connectivity graph formed will be assigned a cost function. This cost is the distance of the trapezoid mid-points, weighted by the sheet resistance of the routing layer.
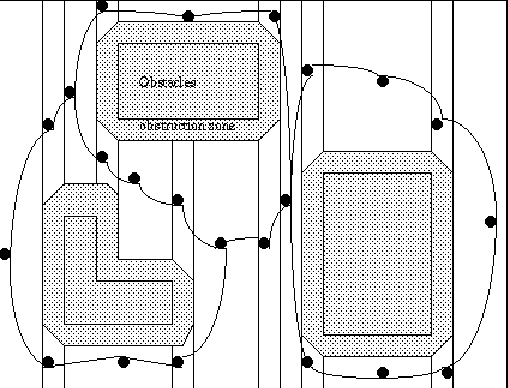
Figure 4 : Regions after linking the obstacles to form a connectivity graph
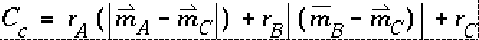
where
By examining the information in (4), we can determine for each node in the graph, which nets out of (2) will be entering or leaving the node. The above information is depicted in the following table :
Table 1 : Information about the in-nets and out-nets for each dissected sub-region
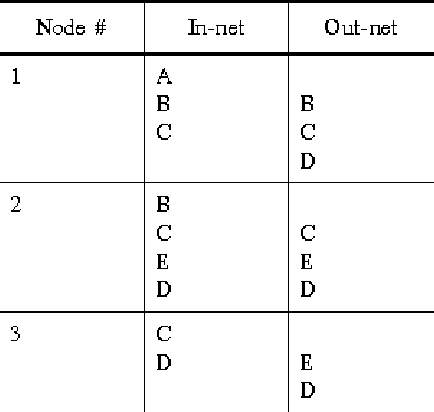
Furthermore, it is also possible to know the starting node and the ending node of each net based on the above information. This is useful because one of the consequences of region decomposition is the segmentation of each original net to be routed. It is not hard to see that the routing of the starting and ending net segment of any original net is the easiest. This will simplify the analysis to be done on each node discussed below.
In the following discussion, we will transform each node in the connectivity graph back to its original shape (assume trapezoid from now on), We will need to do a detailed routing on each node to complete all the net connections.
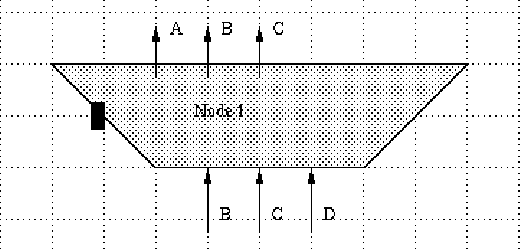
Figure 5 Assuming that we are doing a vertical scan on the region, then each net can only enter or leave the trapezoid from above or below. Only the pins on the left or right side of the trapezoid are `real', the ones on the top or bottom are pseudo pins, in a sense that while we are aware of their existence along the entrance and exit, their exact position are yet to be determined.
There are three different kinds of nets that may be present in the trapezoid :
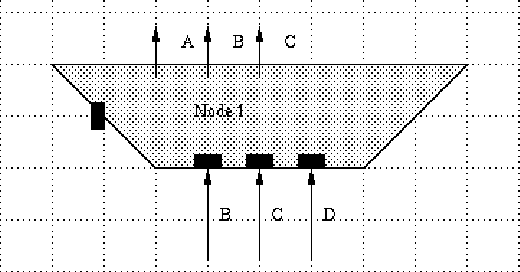
Figure 6
We will then route those nets that begin or terminate inside the trapezoid, To leave the most open space for any subsequent routing, we will route those nets along the boundary of the trapezoid (Figure 7).
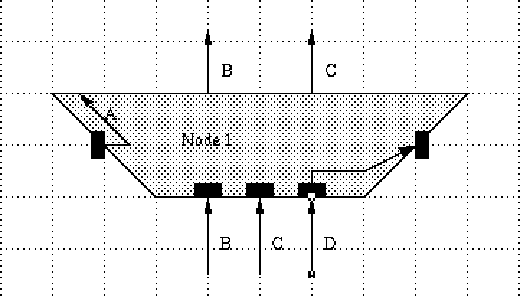
Figure 7
The routing or the remaining nets proceeds as followed :
Determine the position of the trapezoid to be entered with respect to the current trapezoid.
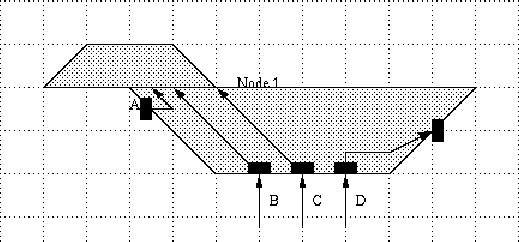
Figure 8
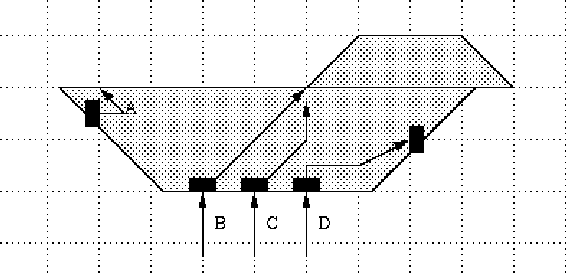
Figure 9
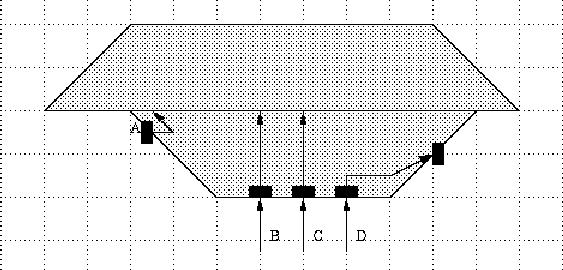
Figure 10
To ease our implementation, a well-defined user input format is very much appreciated. Moreover, the sets of design rule that we need to take into consideration should also be clearly stated.
To measure the quality of our prototype router, sample problems should be provided especially those large test cases. If possible, we would like to have the results obtained by using other routers.
Any suggestions or comments are very much welcomed and can be sent to the following email addresses :
 Back to home page.
Back to home page.