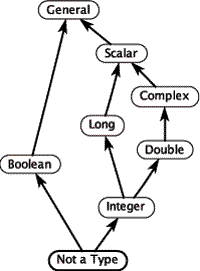
Figure 1: A type lattice
Center for Hybrid and Embedded Software Systems (CHESS), National Science Foundation 0720882 (CSR-EHS: PRET), National Science Foundation 1035672 (CPS: PTIDES), National Science Foundation 0931843 (ActionWebs), Multiscale Systems Center (MuSyC), Army Research Office W911NF-11-2-0038 (DDoSoS), Air Force Research Lab, Robert Bosch GmBH, National Instruments, Thales and Toyota
The Ptolemy Hierarchical Orthogonal Multi-Attribute Solver (PtHOMAS) is a collaborative project with CHESS partner Bosch through the Bosch Research and Technology Center. This work was supported in part by the Center for Hybrid and Embedded Software Systems (CHESS) at UC Berkeley, which receives support from the National Science Foundation (NSF awards #0720882 (CSR-EHS: PRET), #1035672 (CPS: PTIDES) and #0931843 (ActionWebs)), the U. S. Army Research Office (ARO #W911NF-11-2-0038), the Air Force Research Lab (AFRL), the Multiscale Systems Center (MuSyC), one of six research centers funded under the Focus Center Research Program, a Semiconductor Research Corporation program, and the following companies: Bosch, National Instruments, Thales, and Toyota.
This project is focused on enhancing model-based design techniques with the ability to include in models semantic information about data (what the data means), to check consistency in the usage of data across models, find bugs in interfaces between models, and to improve communication across teams.
The approach is to build on classical data type systems, which address this problem up to a point. It is easy to check, for example, whether two models agree that a variable represents an integer value. But additional meaning like the units and the semantic interpretation of the data is not captured in the type system. An organization of such meaning is referred to in computer science as a data ontology.
In classical type systems, the relationship between types form a partial order, or more specifically, a mathematical lattice, as shown in figure 1, "A type lattice", for a small subset of a typical type system. Type checking and type inference algorithms are based on efficient algorithms for solving systems of inequalities over such partial orders.
A data ontology can be similarly constructed as a lattice, as shown in figure 2 "A data ontology". In this example, each node in the ontology specifies an interpretation of a piece of data and the relations between nodes indicate "is a" relationships between these interpretations. In the PtHOMAS project, we associate such ontologies with models and apply consistency checks, inference algorithms, and model optimizations based on the results of the inference.
Figure 3 shows a constant propagation ontology. This ontology represents a signal value that may either have a constant value or a non-constant value. The middle element (Constant_x) actually represents an infinite list of incomparable elements parametrized by their values, but this does not change the lattice structure.
Using this ontology, inference can be used to determine that the output of a model is non-constant (Figure 4), or it can determine that the output is constant and infer what that value would be (Figure 5). This type of analysis is much like constant propagation analyses in compilers, but is more general as it can be defined by the users of our PtHOMAS framework.

Figure 1: A type lattice
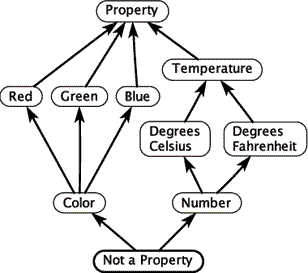
Figure 2: A data ontology
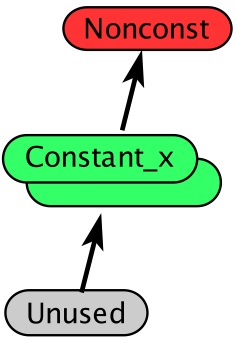
Figure 3: An ontology for constant propagation.
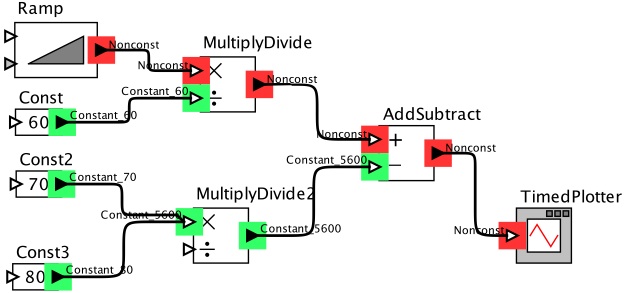
Figure 4: A model whose output can be inferred to be non-constant.
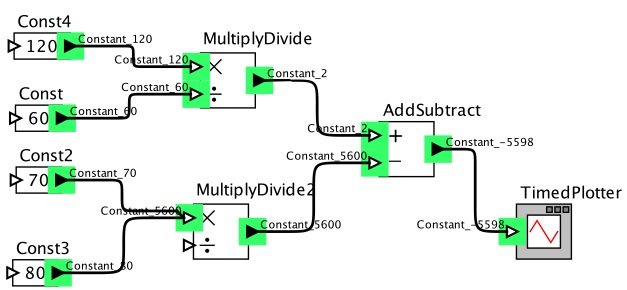
Figure 5: A model whose output can be inferred to be a specific constant value.
1Bosch
2Bosch
More information: http://chess.eecs.berkeley.edu/pthomas