Mapping Multiple Independent Synchronous Dataflow Graphs

4 Scheduling implications

Before we discuss methods for scheduling multiple graphs on one processor, we must define what it means to fire a graph. We define a firing of an SDF graph to be one schedule period of an SDF schedule where each of the actors is fired the number of times specified by the minimal repetitions vector. For example, for the graph in figure 2 the schedule given was AABAB. One iteration of this schedule would be a firing. However, another valid SDF schedule that does not obey our definition of a firing is AABAABAABB. Here, the schedule is a valid SDF schedule in that it returns the arc to its initial number of tokens. However, the schedule contains more repetitions of each actor than are required.

4.1 Static scheduling

In the explicit case, the user specifies how many times each graph is fired relative to the other. For example, in figure 3, the user could specify that graph AB is to fire 160 times for every 147 times graph CDE is to fire. So a valid static schedule for the processor is, 160(3(A)2(B))147(CDE).

In the implicit case, the graphs would contain actors that require firing at a certain rate relative to a global clock. For example, if actor A reads in samples at 48 kHz and actor C writes samples at 44.1 kHz. The graph AB would have to fire 160 times for 147 firings of CDE. One possible valid static schedule for the processor is, 160(3(A)2(B))147(CDE).

The timing requirements of graph AB may not allow the long delay (147 firings of CDE) between the 160th and 161st firings of the graph. The schedule 13(3(A)2(B))147(3(A)2(B)CDE) reduces the delay to one firing of CDE. The timing requirements may be so strict that not even one complete firing of CDE is allowed between firings of graph AB. A more fine-grain interleaving, such as 13(3(A)2(B))147(ACADABEB), may be required in this case.

4.2 Dynamic scheduling

If the uncertainty in the relative rates is small, for example AB fires 160 or 161 times for every 147 firings of CDE, then the methods described by Kuroda and Nishitani [10] could be used. A set of 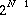static schedules is constructed for a N-task system. In this case, the two schedules would be 160(3(A)2(B))147(CDE) and 161(3(A)2(B))147(CDE). Measurements from a hardware timer determine which of these schedules is executed next. The major drawback of this approach is that the complexity grows exponentially with the number of tasks.

A more general dynamic scheduling scheme could use a real-time operating system that provides prioritized, preemptive scheduling. By using rate-monotonic priority assignment [9], in which tasks with higher rates are given higher priority, the operating system will provide the necessary run-time interleaving in such a way that all deadlines will be met if possible. If bounds on the firing rates and execution times of the tasks are available, then it is possible to guarantee that all deadlines will be met.

Preemptive rate-monotonic scheduling can be useful even with incomplete timing information. Because priorities are fixed, it is possible to predict which tasks will miss their deadlines in an overload situation. Firing rates need not be known exactly as long as there is an ordering of the rates. Execution times, which can be difficult to accurately estimate for programs written in C or other high level languages, are not used in the priority assignments.

Such a solution is attractive for its simplicity, but a large overhead is incurred for the operating system. Separate stacks must be maintained for the different tasks, and a large amount of context must be saved and restored when switching tasks. To avoid this overhead, a simple non-preemptive multitasking kernel can be used with rate-monotonic priorities[11]. By restricting the points at which a context switch is allowed to occur, a single system-wide stack will suffice and the context that must be saved and restored will be lighter, consisting of just a few machine registers.

[Next] [Previous] [Top]