7  Defining Functions

The expression language supports definition of functions. The syntax is:

 
function(arg1:Type, arg2:Type...)
   function body 

where function' is the keyword for defining a function. The type of an argument can be left unspecified, in which case the expression language will attempt to infer it. The function body gives an expression that defines the return value of the function. The return type is always inferred based on the argument type and the expression. For example:

 
function(x:double) x*5.0

defines a function that takes a double argument, multiplies it by 5.0, and returns a double. The return value of the above expression is the function itself. Thus, for example, the expression evaluator yields:

>> function(x:double) x*5.0
(function(x:double) (x*5.0))

To apply the function to an argument, simply do

>> (function(x:double) x*5.0) (10.0) 
50.0

Alternatively, in the expression evaluator, you can assign the function to a variable, and then use the variable name to apply the function. For example,

>> f = function(x:double) x*5.0
(function(x:double) (x*5.0))
>> f(10) 
50.0

Functions can be passed as arguments to certain higher-order functions" that have been defined (see Table 19) . For example, the iterate() function takes three arguments, a function, an integer, and an initial value to which to apply the function. It applies the function first to the initial value, then to the result of the application, then to that result, collecting the results into an array whose length is given by the second argument. For example, to get an array whose values are multiples of 3, try

>> iterate(function(x:int) x+3, 5, 0)
{0, 3, 6, 9, 12}

The function given as an argument simply adds three to its argument. The result is the specified initial value (0) followed by the result of applying the function once to that initial value, then twice, then three times, etc.

Another useful higher-order function is the map() function. This one takes a function and an array as arguments, and simply applies the function to each element of the array to construct a result array. For example,

>> map(function(x:int) x+3, {0, 2, 3})
{3, 5, 6}

A typical use of functions in a Ptolemy II model is to define a parameter in a model whose value is a function. Suppose that the parameter named f has value function(x:double)x*5.0. Then within the scope of that parameter, the expression f(10.0) will yield result 50.0.

Functions can also be passed along connections in a Ptolemy II model. Consider the model shown in figure 6. In that example, the Const actor defines a function that simply squares the argument. Its output, therefore, is a token with type function. That token is fed to the "f" input of the Expression actor. The expression uses this function by applying it to the token provided on the "y" input. That token, in turn, is supplied by the Ramp actor, so the result is the curve shown in the plot on the right.

Figure 6: Example of a function being passed from one actor to another

A more elaborate use is shown in figure 7 In that example, the Const actor produces a function, which is then used by the Expression actor to create new function, which is then used by Expression2 to perform a calculation. The calculation performed here adds the output of the Ramp to the square of the output of the Ramp.

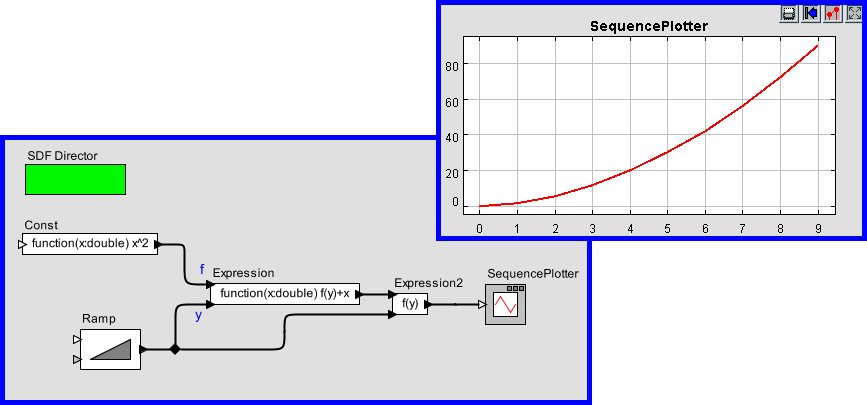Figure 7: More elaborate example with functions passed between actors

Functions can be recursive, as illustrated by the following (rather arcane) example:

>> fact = function(x:int,f:(function(x,f) int)) (x<1?1:x*f(x-1,f))
(function(x:int, f:function(a0:general, a1:general) int) (x<1)?1:(x*f((x-1), f)))
>> factorial = function(x:int) fact(x,fact)
(function(x:int) (function(x:int, f:function(a0:general, a1:general) int)
 (x<1)?1:(x*f((x-1), f)))(x, (function(x:int,
 f:function(a0:general, a1:general) int) (x<1)?1:(x*f((x-1), f)))))
>> map(factorial, [1:1:5].toArray())
{1, 2, 6, 24, 120}

The first expression defines a function named "fact" that takes a function as an argument, and if the argument is greater than or equal to 1, uses that function recursively. The second expression defines a new function "factorial" using "fact." The final command applies the factorial function to an array to compute factorials.