7.1 Introduction

The dynamic dataflow (DDF) domain in Ptolemy is a superset of the synchronous dataflow (SDF) and Boolean dataflow (BDF) domains. In the SDF domain, a star consumes and produces a fixed number of particles per invocation (or "firing"). This static information (the number of particles produced or consumed for each star) makes possible compile-time scheduling. In the BDF domain, some actors with data-dependent production or consumption are allowed. The BDF schedulers attempt to construct a compile-time schedule; however, they may fail to do so and fall back on a DDF scheduler. In the DDF domain, the schedulers make no attempt to construct a compile-time schedule. For this reason, there are few constraints on the production and consumption behavior of stars in this domain.

In DDF, a run-time scheduler detects which stars are runnable and fires them one by one until no star is runnable (the system is deadlocked), or until a specified stopping condition has been reached. A star is runnable if it has enough data on its inputs to satisfy its requirements. Thus, the only constraint on DDF stars is that they must specify on each firing how much data they require on each input to be fired again later.

In practice, stars in the DDF domain are written in a slightly simpler way. They are either SDF stars, in which case the number of particles required at each input is a constant, or they are dynamic, in which case they always alert the scheduler before finishing a firing that to be refired they expect some specific number of particles on one particular input. The input that a star is waiting for data on is called the waitPort.

Since the DDF domain is a superset of the SDF domain, all SDF stars can be used in the DDF domain. Similarly for BDF stars. Besides the SDF stars, the DDF domain has some DDF-specific stars that will be described in this chapter. The DDF-specific stars overcome the main modeling limitation of the SDF domain in that they can model dynamic constructs such as conditionals, data-dependent iteration, and recursion. All of these except recursion are also supported by the BDF domain. It is even possible, in principle, to dynamically modify a DDF graph as it executes (the implementation of recursion does exactly this). The lower run-time efficiency of dynamic scheduling is the cost that we have to pay for the enhanced modeling power.

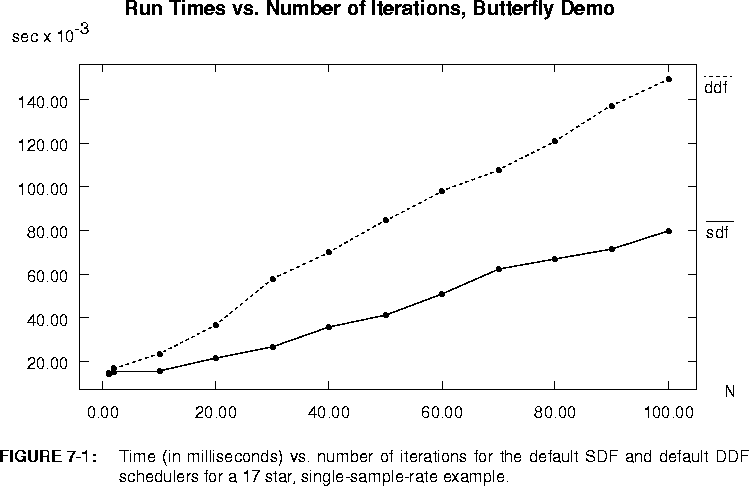
Run-time scheduling is expensive. In figure

7-1 we have plotted the execution time of a simple example (setup and run, not including the pigi "compile" or the wrapup). The example contains 17 stars, all simple, all homogeneous synchronous dataflow (producing or consuming a single sample at each port). The tests were run on a Sparc 10 using the ptrim executable (on August 26, 1995). The default schedulers in the SDF and DDF domains were used. Note that both schedulers took approximately 13ms at startup, and then exhibited a close to linear increase in execution time. For the SDF scheduler, the slope is approximately 650 µs per iteration, while for the DDF scheduler, it is approximately 1,370 µs per iteration. With 17 stars, this comes to about 38 µs per firing for SDF and 81 µs per firing for DDF. For multirate systems, both of these schedulers will perform poorly compared to the loop scheduler in SDF. Note that for this simple system, DDF is more than twice as expensive as SDF. For systems that require DDF, Ptolemy allows us to regain much of this efficiency by grouping SDF stars in a wormhole that contains an SDF domain. For critical systems that are executed for many iterations, this can provide for considerably faster execution.

There are some subtleties, however, in DDF scheduling. Due to these subtleties, there have been three DDF schedulers implemented, all accessible by setting appropriate target parameters. In the next section, we explain these schedulers.