7.2 The DDF Schedulers

In Ptolemy, a scheduler determines the order of execution of blocks. This would seem to be a simple task in the DDF domain, since there is nothing to do at setup time, and at run time, the scheduler only needs to determine which blocks are runnable and then fire those blocks. Experience dictates, however, that this simple-minded policy is not adequate. In particular, it may use more memory than is required (it may even require an unbounded amount of memory when a bounded amount of memory would suffice). It may also be difficult for a user to specify for how long an execution should proceed.

In the SDF domain, an iteration is well-defined. It is the minimum number of firings that brings the buffers back to their original state. In SDF, this can be found by a compile-time scheduler by solving the balance equations. In both BDF and DDF, it turns out that it is undecidable whether such a sequence of firings exists. This means that no algorithm can answer the question for all graphs of a given size in finite time. This explains, in part, why the BDF domain may fail to construct a compile-time schedule and fall back on the DDF schedulers.

We have three simple and obvious criteria that a DDF scheduler should satisfy:

: a. The scheduler should be able to execute a graph forever if it is possible to execute a graph forever. In particular, it should not stop prematurely if there are runnable stars.
: b. The scheduler should be able to execute a graph forever in bounded memory if it is possible to execute the graph forever in bounded memory.
: c. The scheduler should execute the graph in a sequence of well-defined and determinate iterations so that the user can control the length of an execution by specifying the number of iterations to execute.

Somewhat surprisingly, it turns out to be extremely difficult to satisfy all three criteria at once. The first few versions of the DDF scheduler (up to and including release 0.5.2) did not satisfy (b) or (c). The older scheduler is still available (set the useFastScheduler target parameter to YES), but its use is not recommended. Its behavior is somewhat unpredictable and sometimes counterintuitive. For example, told to run a graph for one iteration, it may in fact run it forever. Nonetheless, it is still available because it is significantly faster than the newer schedulers. We have not found a way (yet) to combine its efficient and clever algorithm with the criteria above.

The reason that these criteria are hard to satisfy is fundamental. We have already pointed out that it is undecidable whether a sequence of firings exists that will return the graph to its original state. This fact can be used to show that it is undecidable whether a graph can be executed in bounded memory. Thus, no finite analysis can always guarantee (b). The trick is that the DDF scheduler in fact has infinite time to run an infinite execution, so, remarkably, it is still possible to guarantee condition (b). The new DDF schedulers do this.

Regarding condition (a), it is also undecidable whether a graph can be executed forever. This question is equivalent to the halting problem, and the DDF model of computation is sufficiently rich that the halting problem cannot always be solved in finite time. Again, we are fortunate that the scheduler has infinite time to carry out an infinite execution. This is really what we mean by dynamic scheduling!

Condition (c) is more subtle and centers around the desire for determinate execution. What we mean by this, intuitively, is that a user should be able to tell immediately what stars will fire in one iteration, knowing the state of the graph. In other words, which stars fire should not depend on arbitrary decisions made by the scheduler, like the order in which it examines the stars.

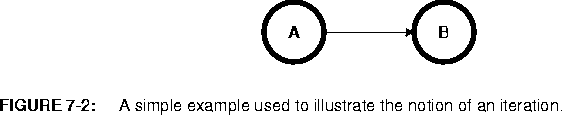
To illustrate that this is a major issue, suppose we naively define an iteration to consist of "firing all enabled stars at most once." Consider the simple example in figure

7-2. Star A is enabled, so we can fire it. Suppose this makes star B enabled. Should it be fired in the same iteration? Will the order in which we fire enabled stars or determine whether stars are enabled impact the outcome?

We have implemented two policies in DDF. These are explained below.

7.2.1 The default scheduler

The default scheduler, realized in the class DDFSimpleSched, first scans all stars and determines which are enabled. In a second pass, it then fires the enabled stars. Thus, the order in which the stars fire has no impact on which ones fire in a given iteration.

Unfortunately, as stated, this simple policy still does not work. Suppose that star A in figure 7-2 produces two particles each time it fires, and actor B consumes 1. Then our policy will be to fire actor A in the first iteration and both A and B in all subsequent iterations. This violates criterion (b), because it will not execute in bounded memory. More importantly, it is counterintuitive. Thus, the DDFSimpleSched class implements a more elaborate algorithm.

One iteration, by default, consists of firing all enabled and non-deferrable stars once. If no stars fire, then one deferrable star is carefully chosen to be fired. A deferrable star is one with any output arc (except a self-loop) that has enough data to satisfy the destination actor. In other words providing more data on that output arc will not help the downstream actor become enabled; it either already has enough data, or it is waiting for data on another arc. If a deferrable star is fired, it will be the one that has the smallest maximum output buffer sizes. The algorithm is formally given in figure

7-3.

This default iteration is defined to fire actors at most once. Sometimes, a user needs several such basic iterations to be treated as a single iteration. For example, a user may wish for a user iteration to include one firing of an XMgraph star, so that each iteration results in one point plotted. The basic iteration may not include one such firing. Another more critical example is a wormhole that contains a DDF system but will be embedded in an SDF system. In this case, it is necessary to ensure that one user iteration consists of enough firings to produce the expected number of output particles.

This larger notion of an iteration can be specified using the target pragma mechanism to identify particular stars that must fire some specific number of times (greater than or equal to one) in each user iteration. To use this, make sure the domain is DDF and the target is DDF-default. Then in pigi, place the mouse over the icon of the star in question, and issue the edit-pragmas command ("a"). One pragma (the one understood by this target) will appear; it is called firingsPerIteration. Set it to the desired value. This will then define what makes up an iteration.

7.2.2 The clustering scheduler

If you set the target parameter restructure to YES, you will get a scheduler that clusters SDF actors when possible and invokes the SDF scheduler on them. The scheduler is implemented in the class DDFClustSched. WARNING: As of this writing, this scheduler will not work with wormholes, and will issue a warning. Nonetheless, it is an interesting scheduler for two reasons, the first of which is its clustering behavior. The second is that it uses a different definition of a basic iteration. In this definition, a basic iteration (loosely) consists of as many firings as possible subject to the constraint that no actor fires more than once and that deferrable actors are avoided if possible. The complete algorithm is given in figure

7-4. Use of this scheduler is not advised at this time, however. For one thing, the implementation of clustering adds enough overhead that this scheduler is invariably slower than the default scheduler.

7.2.3 The fast scheduler

In case the new definition of an iteration is inconvenient for legacy systems, we preserve an older and faster scheduler that is not guaranteed to satisfy criteria (b) and (c) above. The basic operation of the fast scheduler is to repeatedly scan the list of stars in the domain and execute the runnable stars until no more stars are runnable, with certain constraints imposed on the execution of sources. For the purpose of determining whether a star is runnable, the stars are divided into three groups. The first group of the stars have input ports that consume a fixed number of particles. All SDF stars, except those with no input ports, are included in this group. For this group, the scheduler simply checks all inputs to determine whether the star is runnable.

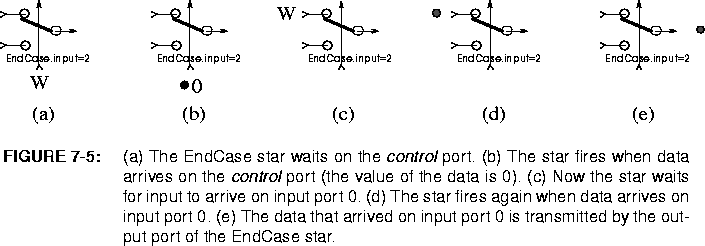
The second group consists of the DDF-specific stars where the number of particles required on the input ports is unspecified. An example is the EndCase star (a multi-input version of the BDF Select star). The EndCase star has one control input and one multiport input for data. The control input value specifies which data input port requires a particle. Stars in this group must specify at run time how many input particles they require on each input port. Stars specify a port with a call to a method called waitPort and the number of particles needed with a call to waitNum. To determine whether a star is runnable, the scheduler checks whether a specified input port has the specified number of particles.

For example, in the EndCase star, the waitPort points to the control input port at the beginning. If the control input has enough data (one particle), the star is fired. When it is fired, it checks the value of the particle in the control port, and changes the waitPort pointer to the input port on which it needs the next particle. The star will be fired again when it has enough data on the input port pointed by waitPort. This time, it collects the input particle and sends it to the output port. See Figure 7-5.

The third group of stars comprises sources. Sources are always runnable. Source stars introduce a significant complication into the DDF domain. In particular, since they are always runnable, it is difficult to ensure that they are not invoked too often. This scheduler has a reasonable but not foolproof policy for dealing with this. Recall that the DDF domain is a superset of the SDF domain. The definition of one iteration for this scheduler tries to obtain the same results as the SDF scheduler when only SDF stars are used. In the SDF domain, the number of firings of each source star, relative to other stars, is determined by solving the balance equations. However, in the DDF domain, the balance equations do not apply in the same form ¹. The technique we use instead is lazy-evaluation.

Lazy evaluation

At the beginning of each iteration of a DDF application, we fire all source stars exactly once, and temporarily declare them "not runnable." We also fire all stars that have enough initial tokens on their inputs. After that, the scheduler starts scanning the list of stars in the domain. If a star has some particles on some input arcs, but is not runnable yet, then the star initiates the (lazy) evaluation of those stars that are connected to the input ports requiring more data. This evaluation is "lazy" because it occurs only if the data it produces are actually needed. The lazy-evaluation technique ensures that the relative number of firings of source stars is the same under the DDF scheduler as it would be under the SDF scheduler.

We can now define what is meant by one iteration in DDF. An iteration consists of one firing of each source star, followed by as many lazy-evaluation passes as possible, until the system deadlocks. One way to view this (loosely) is that enough stars are fired to consume all of the data produced in the first pass, where the source stars were each fired once. This may involve repeatedly firing some of the source stars. However, a lazy-evaluation is only initiated if a star in need of inputs already has at least one input with enough tokens to fire. Because of this, in some circumstances, the firings that make up an iteration may not be exactly what is expected. In particular, when there is more than one sink star in the system, and the sink stars fire at different rates, the ones firing at higher rates may not be fired as many times as expected. It is also possible for one iteration to never terminate.

When a DDF wormhole is invoked, it will execute one iteration of the DDF system contained in it. This is a serious problem in many applications, since the user may need more control over what constitutes one firing of the wormhole.

¹ Note that the BDF domain adapts the balance equations to the dynamic dataflow case.