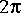







XMgraph star with multiple inputs.FFTCx block will be interpreted as samples of the DTFT in the interval from 0 (d.c.) to 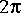
Frequencies in many texts are normalized. To make this exercise more physically meaningful, you should assume a sampling frequency of 128 kHz (
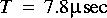
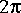
XMGraph star can be used to do this. If the FFT produces 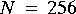

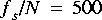
With default parameters, the FFTCx star will read 256 input samples and produce 256 complex output samples. This gives adequate resolution, so just use the defaults for this exercise. The section
"Iterations in SDF" on page 5-3 will tell you, for instance, that you should run your systems for one iteration only. The section
"Particle types" on page 2-20 explains how to properly manage complex signals. For this exercise, you should only plot the magnitude of the FFTCx output, ignoring the phase.
The overall goal is to build a modulation system that transmits a speech or music signal
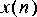

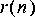
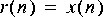
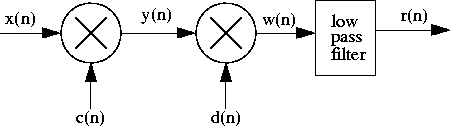
1. The first task is to figure out how to use the FFTCx star to plot the magnitude of a DTFT. Begin by generating a signal where you know the DTFT. Use the Rect star to generate a rectangular pulse
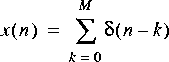
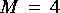
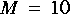
2. The signal generated above does not have narrow bandwidth. The next task will be to generate a signal
RaisedCosine star (found in the "communications" palette). Set the parameters of the RaisedCosine star as follows:3. The next task is to modulate the signal
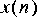
singen galaxy and let it be the carrier 
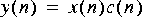
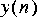
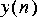
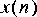
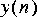
4. The next step it to build the demodulator. First multiply again by the same carrier,
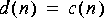
5. To complete the demodulation, you need to filter out the double frequency terms. Use the FIR filter star with its default coefficients. This is not a very good lowpass filter, but it is a lowpass filter. Explain in words exactly how the resulting signal is different from the original baseband signal. How would you make it more like the original? Do you think it is enough like the original to be acceptable for AM broadcasting?

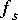
1. The first task is to generate an interesting signal that we can operate on. We will begin with the same signal used in the previous exercise, generated by feeding an impulse into the RaisedCosine star. Set the parameters of the RaisedCosine star as follows:
length: 256
symbol_interval: 8
excessBW: 0.5
interpolation: 1
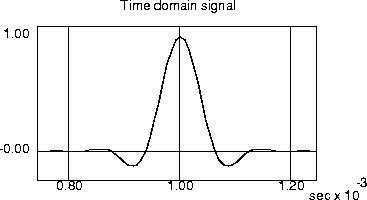
Unlike the previous exercise, you should not leave the interpolation parameter on its default value. The time domain should look like the following (after zooming in on the central portion):
FFTCx to compute and plot the magnitude DTFT, properly labeled in absolute frequency. In other words, instead of the normalized sampling frequency 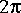
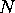
FFTCx star that gets its data should have its size parameter proportional to 1/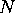
Warning: If you fail to make the numbers consistent, you will either get an error message, or your system will run for a very long time. Please be sure you understand synchronous dataflow. Read
"Iterations in SDF" on page 5-3.
Answer the following questions:
a. Which of the downsampled signals have significant aliasing distortion?
b. What is the smallest sample rate you can achieve with the downsampler without getting aliasing distortion?
3. The next task is to show that sometimes subsampling can be used to demodulate a modulated signal.
a. First, modulate our "interesting signal" with a complex exponential at frequency 32kHz. The complex exponential can be generated using the expgen galaxy in the sources palette. Plot the magnitude spectrum, and explain in words how this spectrum is different from the one obtained in the exercise "Modulation" on page 5-70, which modulates with a cosine at 32kHz.
b. Next, demodulate the signal by downsampling it. What is the appropriate downsampling ratio?
4. The next task is to explore upsampling.
a. First, generate the signal we will work with by downsampling the original "interesting signal" at a 32kHz sample rate (a factor of 4 downsampling). Then upsample by a factor of 4 using the UpSample star. This star will just insert three zero-valued samples for each input sample. Compare the magnitude spectrum of the original "interesting signal" with the one that has been downsampled and then upsampled. Explain in words what you observe.
b. Instead of upsampling with the UpSample star, try using the Repeat star. Instead of filling with zeros, this one holds the most recent value. This more closely emulates the behavior of a practical D/A converter. Set the numTimes parameter to 4. Compare the magnitude spectrum to that of the original signal. Explain in words the difference between the two. Is this a better reconstruction than the zero-fill signal of part (a)?
c. Use the Biquad star with default parameters to filter the output of the Repeat star from part (b). Does this improve the signal? Describe in words how the signal still differs from the original.
1. Generate an exponential sequence
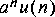
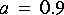
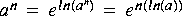
You can use the Const star to generate a constant

Log star, multiply it by the sequence 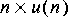
Ramp star, and feed the result into the Exp star. For your display, try the following options to the XMgraph star: "-P -nl -bar".2. A much more elegant way to generate an exponential sequence is to implement a filter with an exponential sequence as its impulse response. Generate the sequence
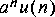
by feeding an impulse (Impulse star) into a first order filter (IIR star). Try various values for

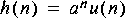
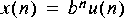
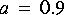
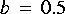
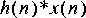
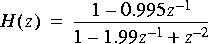
use Ptolemy to find and print the inverse Z transform
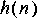
3. Generate the following sequences:
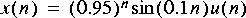
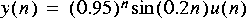
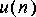
4. Given the following difference equation:

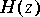
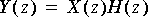
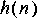
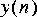
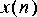
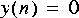
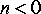
5. This problem explores feedback systems. An example of an "all-pole" filter is
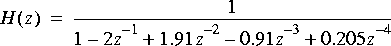
Although there are plenty of zeros (at
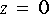
IIR star, you are to implement it using only one or more FIR star(s) in the standard feedback configuration: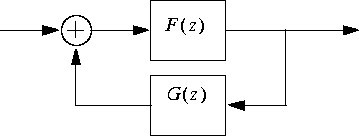
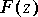
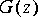
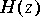
Note: For a feedback system to be implementable in discrete-time, it must have at least one unit delay (
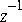
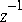
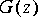
Fork (in the control palette) if you are going to put a delay on a net with more than one destination.FFTCx star. Recall that you will only need to run your system for one iteration when you are using an FFT, or you will get several successive FFT computations. The output of the FFT is complex, but may be converted to magnitude and phase using a complex to real (CxToRect) followed by a rectangular to polar (RectToPolar) converter stars. You can also examine the magnitude in dB by feeding it through the DB star before plotting it.1. Build an FIR filter with real, symmetric tap values. Use any coefficients you like, as long as they are symmetric about a center tap. Look at the phase response. Is it linear, modulo
Unwrap), which attempts to remove the 
2. For the filter you used in (1), what is the group delay? How is the group delay related to the slope of the phase response?
3. Build an FIR filter with odd-symmetric taps (anti-symmetric). Find the phase response of this filter, and compare it to that in (1). Generate a sine wave (using the singen galaxy) and feed it into your filter. What is the phase difference (in radians) between the input cosine and the output? Try different frequencies.
4. Although linear phase is easy to achieve with FIR filters, it can be achieved with other filters using signal reversal. If you run the same signal forwards and backwards through the same filter, you can get linear phase. Given an input
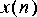
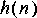
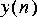
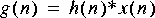
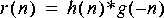
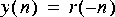
Obviously, this operation is not causal. Let
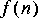
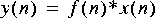
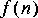
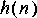
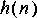
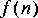
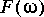
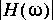
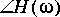
5. All signals in Ptolemy start at time zero, so it is impossible to generate the signal
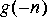
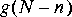
Reverse star. This introduces an extra delay of 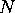
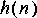
Hint: You will want the block size of the Reverse star to match that used for the FFTCx star. Then just run the system through one iteration. Also, you should delay your impulse into the first filter by half the block size. This will ensure a symmetric impulse response, which is what you want for linear phase. The center of symmetry should be half the block size.
You will experiment with the following transfer function: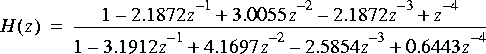
which has the following pole-zero plot:
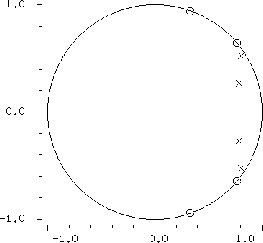
This is a fourth order elliptic filter.
a. Implement this filter in the canonical direct form, or direct form II (using the IIR star). Plot the magnitude frequency response in dB, and verify that it is what you expect from the pole-zero plot.
b. The transfer function can be factored as follows, where the poles nearest the unit circle and the zeros close to those poles appear in the second term:
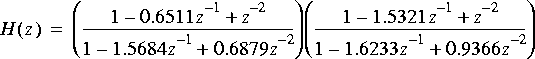
Implement this as a cascade of two second order sections (using two IIR stars). Verify that the frequency response is the same as in part (a). Does the order of the two second order sections affect the magnitude frequency response?
2. You will now quantize the coefficients for implementation in two's complement digital hardware. Assume in all cases that you will use enough bits to the left of the binary point to represent the integer part of the coefficients perfectly. The left-most bit is the most significant bit. You will only vary the number of bits to the right of the binary point, which represent the fractional part. With zero bits to the right of the binary point, you can only represent integers. With one bit, you can represent fractional parts that are either .0 or .5. Other possibilities are given in the table below:
| number of bits right of the binary point | possible values for the fractional part |
|---|---|
| 2 | .0, .25, .5, .75 |
| 3 | .0, .125, .25, .375, .5, .625, .75, .875 |
| 4 | .0, .0625, .125, .1875 .25, .3125, .375, ... |
You can use the IIRFix star to implement this. First, we will study the effects of coefficient quantization only. To minimize the impact of fixed-point internal computations in the IIRFix star, set the InputPrecision, AccumulationPrecision, and OutputPrecision to 16.16 (meaning 16 bits to the right and 16 bits to the left of the binary point) getting more than adequate precision.
a. For the cascaded second-order sections of problem 1a, quantize the coefficients with two bits to the right of the binary point. Compare the resulting frequency response to the original. What has happened to the pole closest to the unit circle? Do you still have a fourth-order system? Does the order of the second order sections matter now?
b. Repeat part (a), but using four bits to the right of the binary point. Does this look like it adequately implements the intended filter?
3. Direct form implementations of filters with order higher than two are especially subject to coefficient quantization errors. In particular, poles may move so much when coefficients are quantized that they move outside the unit circle, rendering the implementation unstable. Determine whether the direct form implementation of problem (1a) is stable when the coefficients are quantized. Try 2 bits to the right of the binary point and 4 bits to the right of the binary point. You should plot the impulse response, not the frequency response, to look for instability. How many bits to the right of the binary point do you need to make the system stable?
4. Experiment with the other precision parameters of the IIRFix star. Is this filter more sensitive to accumulation precision than to coefficient precision?
5. Many applications require a very narrowband lowpass filter, used to extract the d.c. component of a signal. Unfortunately, the pole locations for second-order direct form 2 structures are especially sensitive to coefficient quantization in the region near
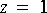
a. The following transfer function is that of a second-order Butterworth lowpass filter:
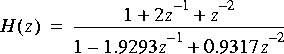
Find and sketch the pole and zero locations of this filter. Compute and plot the magnitude frequency response. Where is the cutoff frequency (defined to be 3dB below the peak)?
b. Quantize the coefficients to use four bits to the right of the binary point. How many bits to the left of the binary point are required so that all the coefficients can be represented in the same format? Compute and plot the magnitude frequency response of this new filter. Explain why it is so different. What is wrong with it?
c. The following transfer function is a bit better behaved when quantized to four bits to the right of the binary point:
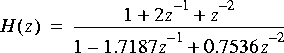
It is also a second order Butterworth filter. Determine where its 3dB cutoff frequency is. Quantize the coefficients to four bits right of the binary point, and determine how closely the resulting filter approximates the original.
d. Use the filter from part (c) (possibly used more than once), together with Upsample and Downsample stars to implement a lowpass filter with a cutoff of 0.05 radians. Implement both the full precision and quantized versions. Describe qualitatively the effectiveness of this design. Your input and output sample rate should be the same, and the objective is to pass only that part of the input below 0.05 radians to the output unattenuated.
1. Use the Rect star to generate rectangular windows of length 8, 16, and 32. Set the amplitude of the windows so that they have the same d.c. content (so that the Fourier transform at zero will be the same).
a. Find the drop in dB at the peak of the first side-lobe in the frequency domain. Also find the position (in Hz, assuming the sampling interval
b. Find the drop in dB at the side-lobe nearest
2. Repeat problem 1 with a Hanning window instead of a rectangular window. Be sure to set the period parameter of the Window star to a negative number in order to get only one instance of the window.
3. An ideal low-pass filter with cutoff at
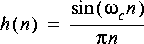
This impulse response can be generated for any range
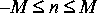
RaisedCosine star from the communications subpalette, or the Sinc star from the nonlinear subpalette. This star is actually an FIR filter, so feed it a unit impulse. Its output will be shaped like 
a. What is the theoretical cutoff frequency
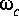
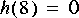
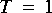
b. Multiply the 64-tap impulse response gotten from the RaisedCosine star by Hanning and steep Blackman windows, and plot the original 64-tap impulse response together with the two windowed impulse responses. Which impulse responses end more abruptly on each end?
c. Compute and plot the magnitude frequency response (in dB) of filters with the three impulse responses plotted in part (b). You will want to change the parameter of the FFTCx star to get more resolution. You can use an order of 9 (which corresponds to a 512 point FFT). You can also set the size to 64 since the input has only 64 non-zero samples. Describe qualitatively the difference between the three filters. What is the loss at
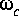
4. In this problem, you will use the rather primitive FIR filter design software provided with Ptolemy. The program you will use is called "optfir"; it uses the Parks-McClellan algorithm to design equiripple FIR filters. See
"optfir - equiripple FIR filter design" on page C-1 for an explanation of how to use it. The main objective in this problem will be to compare equiripple designs to the windowed designs of the previous problem.
b. The filter you designed in part (a) should end up having a slightly wider passband than the designs in problem 3. So to make the comparison fair, we should use a passband edge smaller than (1/16)Hz. Choose a reasonable number to use and repeat your design.
c. Experiment with different transition band widths. Draw some conclusions about equiripple designs versus windowed designs.
FFTCx (complex FFT) and a DTFT star in the "dsp" palette. The FFTCx star has an order parameter and a size parameter. It consumes size input samples and computes the DFT of a periodic signal formed by repeating these samples with period 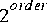
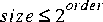
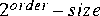
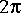
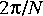
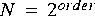
The DTFT star, by contrast, computes samples of the DTFT of a finite input signal at arbitrary frequencies (the frequencies are supplied at a second input port). If you are interested in computing even spaced samples of the DTFT in the whole range from d.c. to the sampling frequency, the DTFT star would be far less efficient than the FFTCx star. However, if you are interested in only a few samples of the DTFT, then the DTFT star is more efficient. For this exercise, you should use the FFTCx star.
1. Find the 8 point DFT (order = 3, size = 8) of each of the following signals:

Plot the magnitude, real, and imaginary parts on the same plot. Ignoring any slight roundoff error in the computer, which of the DFTs is purely real? Purely imaginary? Why? Give a careful and complete explanation. Hint: Do not rely on implicit type conversions, which are tricky to use. Instead, explicitly use the CxToReal and RectToPolar stars to get the desired plots.
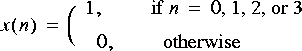
as in (a) above. Compute the 4, 8, 16, 32, and 64 point DFT using the FFTCx star. Plot the 64 point DFT. Explain why the 4 point DFT is as it is, and explain why the progression does what it does as the order of the DFT increases.
3. Assuming a sample rate of 1 Hz, compare the 128 point FFT (order = 7, size = 128) of a 0.125 Hz cosine wave to the 128 point FFT of a 0.123 Hz cosine wave. It is easy to observe the differences in the magnitude, so you should plot only the magnitude of the output of the FFTCx star. Explain why the DFTs are so different.
4. For the same 0.125 Hz signal of problem 3, compute a DFT of order 512 using only 128 samples, padded by zeros (order = 9, size = 128; the zero padding will occur automatically). Explain the difference in the magnitude frequency response from that observed in problem 3. Do the same for the 0.123 Hz signal. Is its magnitude DFT much different from that of the 0.125 Hz cosine? Why or why not?
5. Form a rectangular pulse of width 128 and plot its magnitude DFT using a 512 point FFT (order = 9, size =512). How is this plot related to those in problem 4? Multiply this pulse by 512 samples of a 0.125 Hz cosine wave and plot the 512 point DFT. How is this related to the plot in problem 4? Explain. Reminder: If you get an error message "unresolvable type conflict" then you are probably connecting a float signal to both a float input and a complex input. You can use explicit type conversion stars to correct the problem.
6. To study circular convolution, let
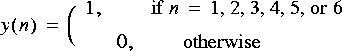
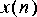
FFTCx star to compute the 8 point circular convolution of these two signals. Which points are affected by the overlap caused by circular convolution? Compute the 16 point circular convolution and compare.1. Implement a filter with two zeros, located at


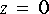
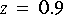
Biquad or IIR star in the "dsp" palette. Filter white noise with it to generate an ARMA process. Then design a whitening filter that converts the ARMA process back into white noise. Demonstrate that your system does what is desired by whatever means seems most appropriate.2. Implement a causal FIR filter with two zeros at
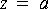
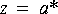
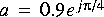
Plot its magnitude frequency response and phase response, using the Unwrap star to remove discontinuities in the phase response. Then implement a second filter with two zeros at 1/a and 1/a*. Adjust the gain of this filter so that it is the same at d.c. as the first filter. Verify that the magnitude frequency responses are the same. Compare the phases. Which is minimum phase? Then implement an allpass filter which when cascaded with the first filter yields the second. Plot its magnitude and phase frequency response.
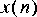
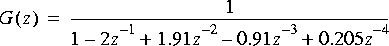
You can implement this with the IIR filter star. The parameters of the star are:
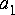
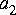
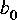
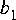
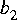
where the transfer function is:

More interestingly, you can implement the filter with an FIR filter in the feedback loop. Try it both ways, but turn in the latter implementation.
2. Define the "desired" signal to be
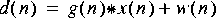
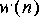
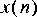
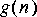
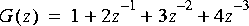
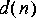
3. Design a Wiener filter for estimating
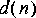
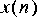
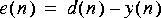
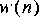
4. Use an adaptive LMS filter to perform the same function as the fixed Wiener filter in part 3. Use the default initial tap values for the LMS filter star. Compare the error signals for the adaptive system to the error signal for fixed system by comparing their power. How closely does the LMS filter performance approximate that of the fixed Wiener filter? How does its performance depend on the adaptation step size? How quickly does it converge? How much do its final tap value look like the optimal Wiener filter solution?
Ptolemy Hint: The powerEst galaxy (in the nonlinear palette) is convenient for estimating power. For the LMS star, to examine the final tap values, set the saveTapsFile parameter to some filename. This file will appear in your home directory (even if you started pigi in some other directory). To examine this file, just type "pxgraph -P filename" in any shell window. The -P option causes each point to shown with a dot. You may also wish to experiment with the LMSTkPlot star to get animated displays of the filter taps as they adapt.
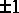
IIDUniform and Sgn stars. This represents a random sequence of bits to be transmitted over a channel. Filter this sequence with the following filter (the same filter used in
"Wiener filtering" on page 5-81): 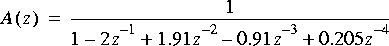
Assume this filter represents a channel. Observe that it is very difficult to tell from the channel output directly what bits were transmitted. Filter the channel output with an LMS adaptive filter. Try two mechanisms for generating the error used to update the LMS filter taps:
a. Subtract the LMS filter output from the transmitted bits directly. These bits may be available at a receiver during a start-up, or "training" phase, when a known sequence is transmitted.
b. Use the Sgn star to make decisions from the LMS filter output, and subtract the filter output from these decisions. This is a decision-directed structure, which does not assume that the transmitted bits are known at the receiver.
To get convergence in reasonable time, it may be necessary to initialize the taps of the LMS filter with something reasonably close to the inverse of the channel response. Try initializing each tap to the integer nearest the optimal tap value. Experiment with other initial tap values. Does the decision-directed structure have more difficulty adapting than the "training" structure that uses the actual transmitted bits? You may wish to experiment with the LMSTkPlot block to get animated displays of the filter taps.
2. For the this problem, you should generate an AR process by filtering Gaussian white noise with the following filter:
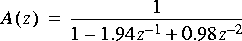
Construct an optimal one-step forward linear predictor for this process using the FIR star, and a similar adaptive linear predictor using the LMS star. Display the two predictions and the original process on the same plot. Estimate the power of the prediction errors and the power of the original process. Estimate the prediction gain (in dB) for each predictor. For each predictor, how many fewer bits would be required to encode the prediction error power vs. the original signal with the same quantization error? Assume the number of bits required for each signal to have the same quantization error is determined by the
3. Modify the AR process so that is generated with the following filter:

Again estimate the prediction gain in both dB and bits. Explain clearly why the prediction gain is so much lower.
4. In the file $PTOLEMY/src/domains/sdf/demo/speech.lin there are samples from two seconds of speech sampled at 8kHz. You need not use all 16,000 samples. The samples are integer-valued with a peak of around 20,000. You may want to scale the signal down. Use your one-step forward linear predictor with the LMS algorithm to compute the prediction error signal. Measure the prediction gain in dB, and note that it varies widely for different speech segments. Identify the segments where the prediction gain is greatest, and explain why. Identify the segments where the prediction gain is small and explain why it is so. Make an engineering decision about the number of bits that can be saved by this coder without appreciable degradation in signal quality. You can read the file using the WaveForm star.
$PTOLEMY/src/domains/sdf/demo/speech.lin, you are to construct an adaptive differential pulse code modulation (ADPCM) coder using the "feedback around quantizer" structure and an LMS filter to form the approximate linear prediction. Be sure to connect your LMS filter so that at the receiver, if there are no transmission errors, an LMS filter can also be used in a feedback path, and the LMS filter will exactly track the one in the transmitter. You will use various amounts of quantization.To assess the ADPCM system, reconstruct the speech signal from the quantized residual, subtract this from the original signal, and measure the noise power. If you have a workstation with a speaker available, listen to the sound, and compare against the original.
1. In your first experiment, do not quantize the signal. Find a good step size, verify that the feedback around quantizer structure works, measure the reconstruction error power and prediction gain. Does your reconstruction error make sense? Compare your prediction gain result against that obtained in the previous lab. It should be identical, since all you have changed is to use the feedback-around-quantizer structure, but you are not yet using a quantizer.
Assume you have a communication channel where you can transmit

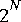
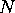

Quant star to accomplish the quantization in both cases. A useful way to set the parameters of the Quant star is as follows (shown for 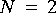
levels: (-1.5*s) (-0.5*s) (0.5*s) (1.5*s)
where "s" is a universe parameter. This way, you can easily experiment with various quantization spacings without having to continually retype long sequences of numbers.
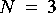
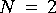
1. In this problem, we study the performance of Burg's algorithm for a simple signal: a sinusoid in noise. First, generate a sinusoid with period equal to 25 samples. Add Gaussian white noise to get an SNR of 10 dB.
a. Using 100 observations, estimate the power spectrum using order 3, 4, 6, and 12th order AR models. You need not turn in all plots, but please comment on the differences.
b. Fix the order at 6, and construct plots of the power spectrum for SNR of 0, 10, 20, and 30 dB. Again comment on the differences.
c. When the AR model order is large relative to the number of data samples observed, an AR spectral estimate tends to exhibit spurious peaks. Use only 25 input samples, and experiment with various model orders in the vicinity of 16. Experiment with various signal to noise ratios. Does noise enhance or suppress the spurious peaks?
d. Spectral line splitting is a well-known artifact of Burg's method spectral estimates. Specifically, a single sinusoid may appear as two closely spaced sinusoids. For the same sinusoid, with an SNR of 30dB, use only 20 observations of the signal and a model order of 15. For this problem, you will find that the spectral estimate depends heavily on the starting phase of the sinusoid. Plot the estimate for starting phases of 0, 45, 90, and 135 degrees of a cosine wave.
2. In this problem, we study a synthetic signal that roughly models both voiced and unvoiced speech.
a. First construct a signal consisting of white noise filtered by the transfer function
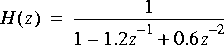
Then estimate its power spectrum using three methods, a periodogram, the autocorrelation method, and Burg's method. Use 256 samples of the signal in all three cases, and order-8 estimates for the autocorrelation and Burg's methods. Increase and decrease the number of inputs that you read. Does the periodogram estimate improve? Do the other estimates improve? How should you measure the quality of the estimates? What order would work better than 8 for this estimate?
b. Instead of exciting the filter
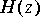
c. Voiced speech is often modeled by an impulse stream into an all-pole filter. Unvoiced speech is often modeled by white noise into an all-pole filter. A reasonable model includes some of both, with more noise if the speech is unvoiced, and less if it is voiced. Mix noise and the periodic impulse stream at the input to the filter
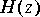
Lattice, RLattice, BlockLattice, and BlockRLattice. The "R" refers to "Recursive", so the "RLattice" stars are inverse filters (IIR), while the "Lattice" stars are prediction-error filters (FIR). The "Block" modifier allows you to connect the LevDur or Burg stars to the Lattice filters to provide the coefficients. A block of samples is processed with a given set of coefficients, and then new coefficients can be loaded.1. Consider an FIR lattice filter with the following values for the reflection coefficients: 0.986959, -0.945207, 0.741774, -0.236531.
a. Is the inverse of this filter stable?
b. Let the transfer function of the FIR lattice filter be written
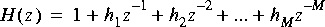
Use the Levinson-Durbin algorithm to find
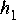
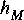
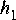
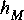
c. Use Ptolemy to verify that an FIR filter with your computed tap values 1,
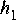
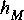
2. In this problem, we compare the biased and unbiased autocorrelation estimates for troublesome sequences.
a. Construct a sine wave with a period of 40 samples. Use 64 samples into the Autocor star to estimate its autocorrelation using both the biased and unbiased estimate. Which estimate looks more reasonable?
b. Feed the two autocorrelation estimates into the LevDur star to estimate predictor coefficients for various prediction orders. Increase the order until you get predictor coefficients that would lead to an unstable synthesis filter. Do you get unstable filters for both biased and unbiased autocorrelation estimates?
c. Add white noise to the sine wave. Does this help stabilize the synthesis filter?
d. Load your reflection coefficients into the BlockLattice star and compute the prediction error both the biased and unbiased autocorrelation estimate. Which is a better predictor?