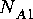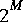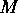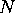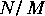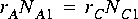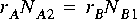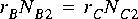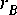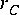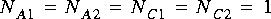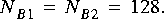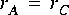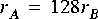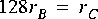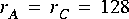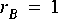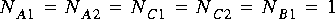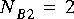
Synchronous dataflow (SDF) is a data-driven, statically scheduled domain in Ptolemy. It is a direct implementation of the techniques given in [Lee87a] and [Lee87b]. "Data-driven" means that the availability of Particles at the inputs of a star enables it. Stars without any inputs are always enabled. "Statically scheduled" means that the firing order of the stars is determined once, during the start-up phase. The firing order will be periodic. The SDF domain is one of the most mature in Ptolemy, having a large library of stars and demo programs. It is a simulation domain, but the model of computation is the same as that used in most of the code generation domains. A number of different schedulers, including parallel schedulers, have been developed for this model of computation.
SDF is a special case of the dataflow model introduced by Dennis [Den75]. It is equivalent to the computation graph model of Karp and Miller [Kar66]. In the terminology of the dataflow literature, stars are called actors. An invocation of the go() method of a star is called a firing. Particles are called tokens. In a digital signal processing system, a sequence of tokens might represent a sequence of samples of a speech signal or a sequence of frames in a video sequence.
When an actor fires, it consumes some number of tokens from its input arcs, and produces some number of output tokens. In synchronous dataflow, these numbers remain constant throughout the execution of the system. It is for this reason that this model of computation is suitable for synchronous signal processing systems, but not for asynchronous systems. The fact that the firing pattern is determined statically is both a strength and a weakness of this domain. It means that long runs can be very efficient, a fact that is heavily exploited in the code generation domains. But it also means that data-dependent flow of control is not allowed. This would require dynamically changing firing patterns. The Dynamic Dataflow (DDF) and Boolean Dataflow (BDF) domains were developed to support this, as described in chapters
7 and
8, respectively.
Each porthole of each SDF star has an attribute that specifies the number of particles consumed (for input ports) or the number of particles produced (for output ports). When you connect two portholes with an arc, the number of particles produced on the arc by the source star may not be the same as the number of particles consumed from that arc by the destination star. To maintain a balanced system, the scheduler must fire the source and destination stars with different frequency.
Consider a simple connection between three stars, as shown in figure
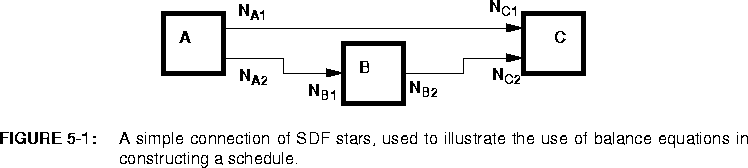5-1. The symbols adjacent to the portholes, such as 
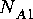, represent the number of particles consumed or produced by that porthole when the star fires. For many signal processing stars, these numbers are simply one, indicating that only a single token is consumed or produced when the star fires. But there are three basic circumstances in which these numbers differ from one:
- Vector processing in the SDF domain can be accomplished by consuming and producing multiple tokens on a single firing. For example, a star that computes a fast Fourier transform (FFT) will typically consume and produce
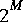samples when it fires, where 
is some integer. Examples of vector processing stars that work this way are FFTCx, Average, Burg, and LevDur. This behavior is quite different from the matrix stars, which operate on particles where each individual particle represents a matrix.
- In multirate signal processing systems, a star may consume
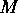samples and produce 
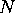, thus achieving a sampling rate conversion of 
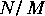. For example, the FIR and FIRCx stars optionally perform such a sampling rate conversion, and with an appropriate choice of filter coefficients, can interpolate between samples. Other stars that perform sample rate conversion include UpSample, DownSample, and Chop.
- Multiple signals can be merged using stars such as
Commutator or a single signal can be split into subsignals at a lower sample rate using the Distributor star.
To be able to handle these circumstances, the scheduler first associates a simple balance equation with each connection in the graph. For the graph in figure
5-1, the balance equations are
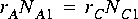
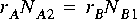
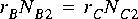
This is a set of three simultaneous equations in three unknowns. The unknowns,
, 
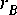, and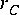 
are the repetitions of each actor that are required to maintain balance on each arc. The first task of the scheduler is to find the smallest non-zero integer solution for these repetitions. It is proven in [Lee87a] that such a solution exists and is unique for every SDF graph that is "consistent," as defined below.
When running an SDF system under the graphical user interface, you will have the opportunity to specify "when to stop." Since the SDF domain has no notion of time, this is not given in units of time. Instead, it is given in units of SDF iterations. At each SDF iteration, each star is fired the minimum number of times to satisfy the balance equations.
Suppose for example that star B in figure
5-1 is an FFTCx star with its parameters set so that it will consume 128 samples and produce 128 samples. Suppose further that star A produces exactly one sample on each output, and star C consumes one sample from each input. In summary,
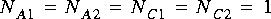
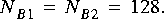
The balance equations become
.
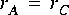
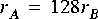
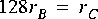The smallest integer solution is
.
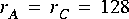
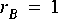Hence, each iteration of the system includes one firing of the FFTCx star and 128 firings each of stars A and B.
It is not always possible to solve the balance equations. Suppose that in figure
5-1 we have
.
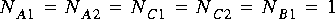
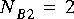In this case, the balance equations have no non-zero solution. The problem with this system is that there is no sequence of firings that can be repeated indefinitely with bounded memory. If we fire A,B,C in sequence, a single token will be left over on the arc between B and C. If we repeat this sequence, two tokens will be left over. Such a system is said to be inconsistent, and is flagged as an error. The SDF scheduler will refuse to run it. If you must run such a system, change the domain of your graph to the DDF domain.
Delays are indicated in Pigi by small green diamonds that are placed on an arc. Most of the standard palettes of stars have the delay icon at the upper left. The delay has a single parameter, the number of samples of delay to be introduced. In the SDF domain, a delay with parameter equal to one is simply an initial particle on an arc. This initial particle may enable a star, assuming that the destination star for the delay arc requires one particle in order to fire. To avoid deadlock, all feedback loops much have delays. The SDF scheduler will flag an error if it finds a loop with no delays. For most particle types, the initial value of a delay will be zero. For particles which hold matrices, the initial value is an empty Envelope, which must be checked for by stars which work on matrix inputs. Initializable delays allow the user to give values to the initial particles placed in the buffer. Please refer to
2.12.8 on page 2-47 for details on how to use initializable delays.
Copyright © 1990-1997, University of California. All rights
reserved.