Modal Models
Modal models combine time-based signals with event sequences within the same state machine, as shown below:
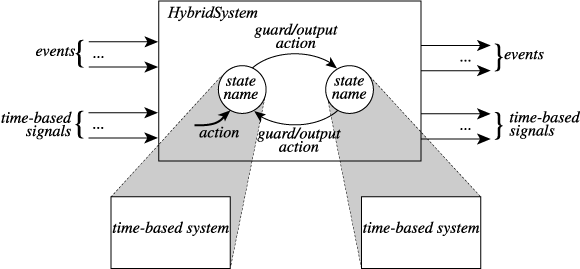
A mode is represented by a state in a finite-state machine that has a refinement that is a time-based system.
- The (complete) state of the hybrid system is a pair (i,s) where i is the mode and s is the state of the time-based refinement system associated with mode i.
- State transitions in the FSM have an action. The action will typically set the initial refinement state of the time-based system in the destination mode.
- The guards are sets of tuples containing event input symbols, time-based input values, and values of the refinement state.
Example: Overload of an electronic system might be modeled by a state transition that is triggered by the magnitude of the current refinement state exceeding some threshold.
- When the system is in some mode, the refinement state is only affected by the time-based inputs. It is not affected by the event inputs. Hence, the time-based refinements donít have to deal with stuttering inputs.
- The FSM may react at any time in the time base. The mode in which it is before this reaction is called the current mode. It will take a discrete state transition and switch to the destination mode if the input values and the refinement state at that time match a guard. If it does not take a discrete state transition, then the FSM stutters. In either case, the refinement of the current mode also reacts to the time-based inputs, changes its state and produces outputs.

 Up to Topics
Up to Topics Previous
Previous Next
Next