EECS20N: Signals and Systems

• Home
• Imaginary numbers
• Imaginary arithmetic
• Complex numbers
• Complex arithmetic
• Exponentials
• Polar coordinates

Polar coordinates

The representation of a complex number as a sum of a real and imaginary number, z = x + iy, is called its Cartesian representation.

Recall from trigonometry that if x, y, r are real numbers and r ² = x ² + y ², then there is a unique number θ with 0 ≤  θ  <  2π such that

cos(θ) = x / r,

sin(θ) = y / r.

That number is

θ	=	cos -1(x / r),
	=	sin -1(y / r)
	=	tan -1(y / x)

We can therefore express any complex number z = x + iy as

z	=	| z | (x / | z | + iy / | z |)
	=	| z | (cos θ + i sin θ)
	=	| z | e iθ ,

where θ = tan ^-1(y / x). The angle or argument θ is measured in radians, and it is written as arg(z). So we have the polar representation of any complex number z as

z = x + iy = re ⁱθ.

The two representations are related by

r = | z | = √(x ² + y ²).

and

θ = arg(z) = tan ^-1(y / x).

The values x and y are called the Cartesian coordinates of z, while r and θ are its polar coordinates. Note that r is real and r ³ 0.

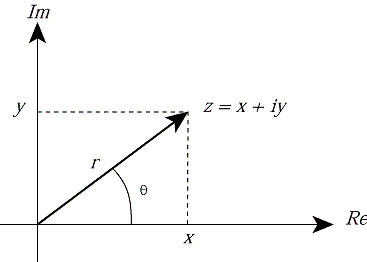
Note that for any integer K,

re ⁱ(2Kπ + θ) = re ⁱθ.

This is because

re ⁱ(2Kπ + θ) = re ⁱ2Kπ e ⁱθ

and

e ⁱ2Kπ = cos (2Kπ) + i sin (2Kπ) = 1.

Thus, the polar coordinates (r, θ) and (r, θ + 2Kπ) for any integer K represent the same complex number. Thus, the polar representation is not unique; by convention, a unique polar representation can be obtained by requiring that the angle given by a value of θ satisfying 0 ≤ θ < 2π or -π < θ ≤ π.

Example 1

The polar representation of the number 1 is 1 = 1 e i0. Notice that it is also true that 1 = 1 e i2π, because the sine and cosine are periodic with period 2π. The polar representation of the number -1 is -1 = 1 e iπ. Again, it is true that -1 = 1 e i3π, or, in fact, -1 = 1 e iπ + K2π for any integer K.

Products

Products of complex numbers represented in polar coordinates are easy to compute. If z_i = r_i e ⁱθ_i , then

z₁ z₂ = r₁ r₂ e ^{i(θ₁ + θ₂ )}

Thus, the magnitude of a product is a product of magnitudes, and the angle of a product is the sum of the angles,

| z₁ z₂ | = | z₁ || z₂ |

arg(z₁ z₂ ) = arg(z₁ ) + arg(z₂ )

Example 2

We can use the polar representation to find the n distinct roots of the equation z n = 1. Write z = re iθ, and 1 = e i2kπ, so z n = r ne inθ = e i2kπ, which gives r = 1 and θ = 2kπ / n, k = 0, 1, ... , n - 1. These are called the n roots of unity.

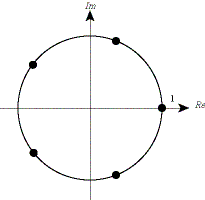
Figure: The 5 roots of unity.