Cascade of LTI Systems is LTI
Consider the cascade of two LTI systems:
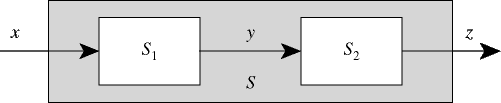
We can show that the composite system is LTI.
Time invariance:
We must show that for any real τ, S . Dτ = Dτ . S. This follows because S1 and S2 are time invariant,
S . Dτ = S2 . S1 . Dτ = S2 . Dτ . S1 = Dτ . S2 . S1 = Dτ . S.
Linearity:
We must show that S(ax1 + bx2) = aS(x1) + bS(x2). This follows because S1 and S2 are linear,
S(ax1 + bx2) = S2(S1(ax1 + bx2))
= S2(aS1(x1) + bS1(x2))
= aS2(S1(x1)) + bS2(S1(x2))
= aS(x1) + bS(x2)

 Up to Topics
Up to Topics Previous
Previous Next
Next