EECS20N: Signals and Systems

Infinite State Systems

We study state machines with

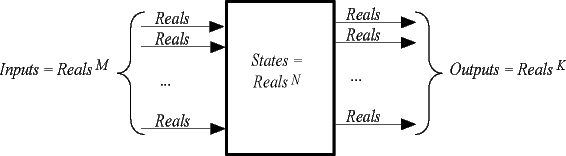
States = Reals N

Inputs = Reals M

Outputs = Reals K

The number of states and the sizes of the input and output alphabets are infinite, which tends to make things more complicated. However, these sets now have arithmetic properties, which opens up a huge new range of modeling and analysis possibilities.

A block diagram of such a system shows the input coming over M input ports and the output delivered over K output ports. (MIMO stands for multi-input, multi-output.)