

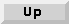






Map star is the most basic of all HOF stars. Its icon is shown below:
$PTOLEMY or ~username. This lends a certain immunity to changes in the filesystem organization. Currently, the file specified must be an oct facet, although in the future, other specifications (like ptcl files) may be allowed. Usually, the oct facet simply contains the definition of the replacement galaxy. If the replacement block is a built-in star, then there is no need to give a value to the where_defined parameter.
The Map star replaces itself in the graph with as many instances of the replacement block as needed to satisfy all of the inputs to the Map star. Consider the example shown in figure
6-1.
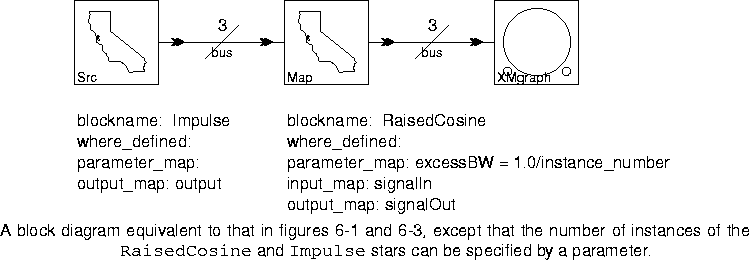
RaisedCosine star. Since this is built-in, there is no need to specify where it is defined, so the where_defined parameter is blank. The RaisedCosine star has a single input named signalIn and a single output named signalOut, so these names are given as the values of the input_map and output_map parameters. The parameter_map parameter specifies the values of the excessBW parameter for each instance of the replacement block to be created; excessBW specifies the excess bandwidth of the raised cosine pulse generated by the star. The syntax of the parameter_map parameter is discussed in detail below, but we can see that the value of the excessBW parameter will be 1.0 for the first instance of the RaisedCosine star, 0.5 for the second, and 0.33 for the third.
The horizontal slash through the last connection on the right in figure
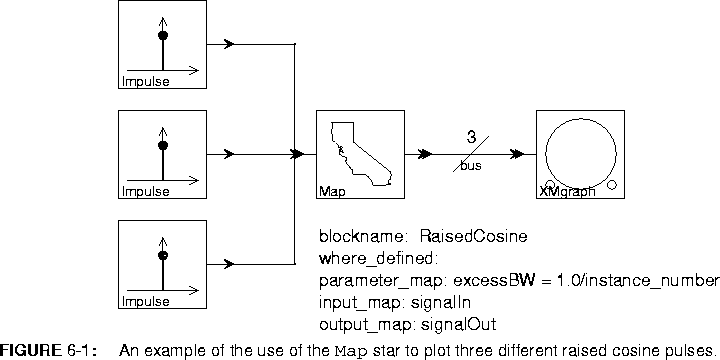
6-1 is a Bus, which is much like a delay in that the icon is placed directly over the arc without any connections. Its single parameter specifies the number of connections that the single wire represents. Here, the bus width has to be three or the Map star will issue an error message. This is because there are three inputs to the Map star, so three instances of the RaisedCosine star will be created. The three outputs from these three instances need somewhere to go. The result of running this system is shown in figure
6-2
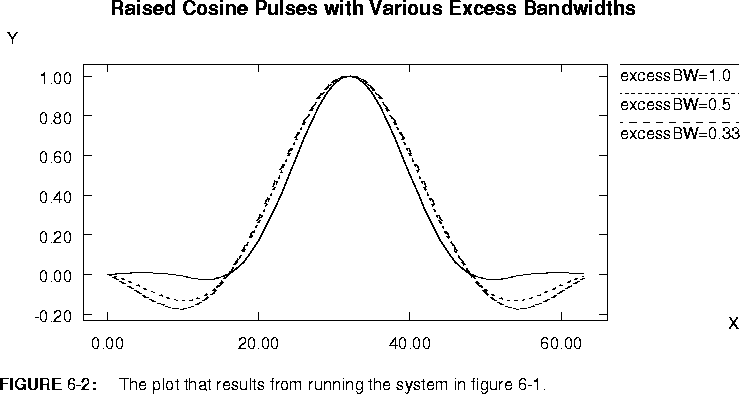
The block diagram in figure 6-1 is equivalent to that in figure 6-3.
Map star has run, the topology of the Ptolemy universe will be exactly as figure
6-3. The Map star itself will not appear in the topology, so examining the topology with, for example, the ptcl print command will not show a Map star instance.
In both figures
6-1 and
6-3, the number of instances of the RaisedCosine star is specified graphically. In figure
6-1, it is specified by implication, through the number of instances of the Impulse star. In figure
6-3 it is specified directly. Neither of these really takes advantage of higher-order functions. The block diagram in figure
6-4
RaisedCosine star. It is only necessary to modify parameters, not the graphical representation. For example, if the value of the bus parameters in figure
6-4 were changed from 3 to 10, the system would then plot ten raised cosines instead of three.
The left-most star in figure
6-4 is a variant of the Map star called Src. It has no inputs, and is used when the replacement block is a pure source block with no input. (This is a separate star type only for historical reasons; a Map icon with zero inputs would work as well. Indeed, for the case of a pure sink replacement block, a Map icon with zero outputs is used.)
Map and Src stars, called MapGr and SrcGr, have the following icons: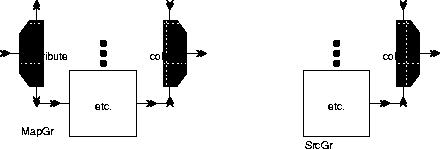
MapGr and SrcGr are single icons, each representing a single star. The complicated shape of the icon is intended to be suggestive of its function when it is found in a block diagram. The MapGr and SrcGr stars work just like the Map and Src stars, except that the user specifies the replacement block graphically rather than textually. For example, the system in figure
6-4 can be specified as shown in figure
6-5.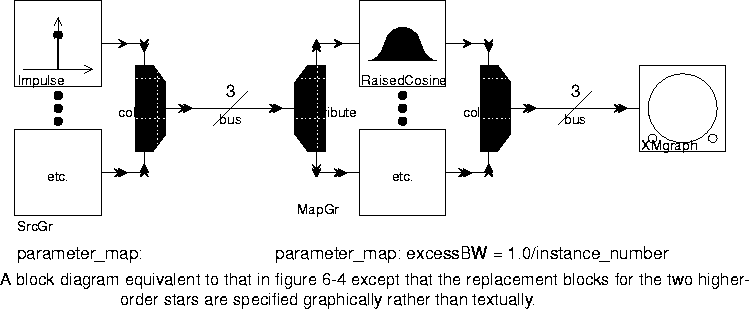
Impulse and RaisedCosine each have one instance wired into the block diagram as an example. Thus, there is no reason for the blockname, where_defined, input_map, or output_map parameters. The MapGr and SrcGr stars have only a single parameter, called parameter_map. The syntax for this parameter is the same as for the Map star, and is fully explained below.
A variant of the MapGr star has the icon shown below:

MapGr star with no outputs.
A more complex application of the MapGr star is shown in figure
6-6.

Commutator, which can take any number of inputs. The bus connected to its input multiporthole determines how many inputs will be used in each instance created by the MapGr star. In the example in figure
6-6, it is set to 2. Thus, each instance of the replacement block processes two input streams and produces one output stream. Consequently, the input bus must be twice as wide as the output bus, or the MapGr star will issue an error message. This example produces the plot shown in figure
6-7.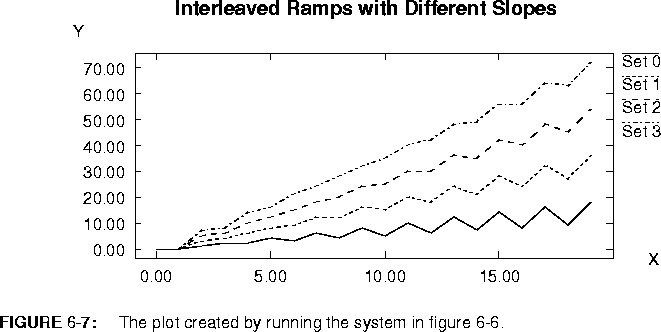
Commutator star, then the output plot will be as shown in figure
6-8.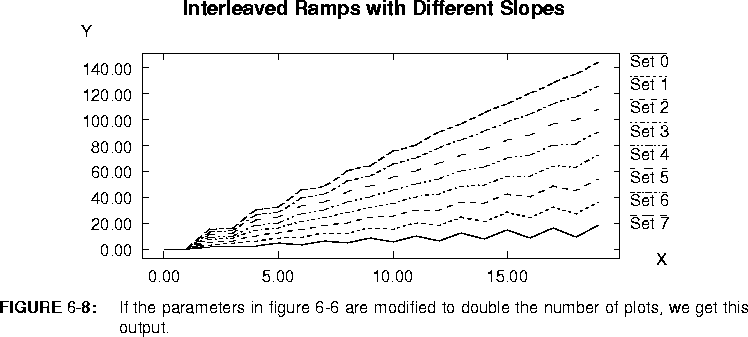
Map star and related stars can be used to set parameter values in the replacement blocks. The parameter_map is a string array, a list of strings. The strings are in pairs, where the pairs are separated by spaces, and there are four acceptable forms for each pair:name value
name(number) value
name = value
name(number) = valueThere should be no spaces between name and (number), and the name cannot contain spaces,
=, or (. In all cases, name is the name of a parameter in the replacement block. In the first and third cases, the value is applied to all instances of the replacement block. In the second and fourth cases, it is applied only to the instance specified by the instance number, (which starts with 1). The third and fourth cases just introduce an optional equal sign, for readability. If the = is used, there must be spaces around it.
The value can be any usual Ptolemy expression for giving the value of a parameter. If this expression has spaces in it, however, then the value should appear in quotation marks so that the whole expression is kept together. If the string instance_number appears anywhere in value, it will be replaced with the instance number of the replacement block. Note that it need not be a separate token. For example, the value xxxinstance_numberyyy will become xxx1yyy for the first instance, xxx2yyy for the second, etc. After all appearances of the string instance_number have been replaced, value is evaluated using the usual Ptolemy expression evaluator for initializing String Array states.
For example, in figure
6-1, the Map star has a blockname of RaisedCosine, and a parameter_map of
excessBW = 1.0/instance_number
When the system is run, the Map star will create three instances of RaisedCosine. The first instance will have its excessBW parameter set to 1.0 (which is 1/1), the second instance of RaisedCosine will have a excessBW of 0.5 (1/2), and the third will have a excessBW of 0.33 (1/3). Since the other RaisedCosine parameters are not mentioned in the parameter_map, they are set to their default values.
As a further example, suppose parameter_map of the Map star in figure
6-1 were set to
excessBW(1) 0.6 excessBW(2) 0.5 excessBW(3) 0.4 length 128
The first RaisedCosine would then have an excessBW of 0.6, the second would have an excessBW of 0.5 and the third would have 0.4 for its excessBW. All three of the RaisedCosine stars would have a length of 128 instead of the default length.
Map star. Suppose the Map star has 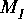
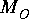
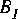


is the number of instances that will be created. This must be an integer. Moreover, the number of input and output connections must be compatible (must satisfy the above equality), or you will get an error message like: "too many inputs for the number of outputs."

Map star will be connected to the inputs of the first instance of the replacement block. To determine in what order these 
Map star will be connected to the next replacement block, again using the ordering specified in input_map. Similarly for the outputs. If there are no inputs at all, then the number of instances is determined by the outputs, and vice versa.
For MapGr and its variants, there is no input_map or output_map parameter; all connections are specified graphically. If the replacement block has more than one input or more than one output port, these connections must be grouped into a bus connection to the appropriate port of the MapGr star. A HOFNop star (see
"Bus manipulation stars" on page 6-13) can be inserted between the MapGr star and the replacement block to perform this grouping. The order of the connections to the Nop star then determines the precise order in which MapGr makes connections. In this way the Nop star's icon provides the same control graphically that input_map and output_map do textually. (By the way, this use of Nop is the only exception to the normal rule that only a single replacement-block icon can be connected to a MapGr star. For both Map and MapGr, if you want to replicate a multiple-star grouping then you need to create a galaxy representing the group to be replicated. The same is true of the remaining HOF stars that generate multiple instances of a block.)
For example, the Add star has a multiple input port named "input". If we want the replacement Add star(s) to have two inputs each, then input_map should be input input. If we want three inputs in each replacement block, then input_map should be input input input. Note that input_map and output_map are both of the String Array type. Thus one can use the shortcut string input[3] instead of the cumbersome input input input string. These two forms are equivalent as input[3] is converted automatically to input input input when the parameter is initialized by Ptolemy.
For MapGr and its variants, the number of connections to a multiporthole of the replacement block is controlled by placing a bus icon on the connection, as was illustrated earlier.
The HOF stars rewire the schematic before any attempt is made to determine porthole types, so the actual assignment of particle types is the same as if the schematic had been written out in full without using any HOF stars.
This was not true in Ptolemy versions prior to 0.7. In prior versions, porthole type assignment occurred before HOF star replacement, which had various unpleasant consequences. For example, the Map star used to constrain its input and output particle types to be the same, which interfered with using a replacement block that changed particle types. Also, it was necessary to have numerous variants of the Src and SrcGr stars, one for each possible output particle type. (If you have any old schematics that contain the type-specific Src or SrcGr variants, you'll need to use masters or ptfixtree to replace them with the generic Src or SrcGr icons.)
MatrixParticle class. This encapsulates a matrix into a single particle. Another alternative is to use the Message class to define your own multidimensional data structure. A third alternative (which is still highly experimental) is to use the multidimensional synchronous dataflow (MDSDF) domain. A fourth alternative, discussed here, is to embed your multidimensional data into one-dimensional streams. Higher-order functions become extremely useful in this case. Our discussion will center on using the SDF domain, although the same principles could be applied in other domains as well.
A two-dimensional array of data can be embedded in a one-dimensional stream by rasterizing it. This means that the sequence in the stream consists of the first row first, followed by the second row, followed by the third, etc. This is one example of a multiprojection, so called because higher-dimensional data is projected onto a one-dimensional sequence. Typically, however, we wish to perform some operations row-wise, and others column-wise, so the rasterized format can prove inconvenient. Row-wise operations are easy if the data is rasterized, but column-wise operations are awkward. Fortunately, in the SDF domain, we can transpose the data with a cascade of two stars, a Distributor and a Commutator, as shown below:
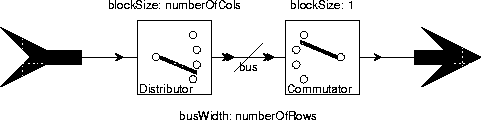
If the input is row-wise rasterized, then the output will be column-wise rasterized, meaning that the first column will come out first, then the second column, then the third, etc. It has been shown that any transposition of any arbitrary multiprojection can be accomplished with such a cascade [Khi94].
As an example of the use of a multi-projection transformation, consider the two-dimensional FFT shown in figure 6-9.

FFTCx star in the SDF domain has two key parameters, the order and the size. The size is the number of input samples read each time the FFT is computed. For the row FFT, this should be equal to the number of columns. These samples are then padded with zeros (if necessary) to get a total of 2order samples. The FFTCx star then computes a 2order point FFT, producing 2order complex outputs. In figure
6-9, these outputs are then transposed so that they are column-wise rasterized. The second FFTCx star then computes the FFT of the columns. The output is column-wise rasterized.The effect of a transposition can be accomplished using higher-order functions in a way that is sometimes more intuitive. In particular, a matrix can be represented as a bus, where each connection in the bus carries one row, and the width of the bus is the number of rows. To make this concrete, the same two-dimensional FFT is re-implemented in figure 6-10

MapGr star is then used to apply the FFT to each signal in the bus. The results are recombined in column-wise rasterized format, and the column FFT is computed.Map star and its variants apply instances of their replacement block in parallel to the set of input streams. Another alternative is provided by the Chain star, which strings together some specified number of instances of the replacement block in series. The parameters are similar to those of the Map star, except for the addition of internal_map. The internal_map parameter specifies connections made between successive instances of the replacement block in the cascade. It should consist of an alternating list of output and input names for the replacement block.
An example of the use of the Chain star is a string of biquad filters in series. The IIR filter star, which can be used to create a biquad filter, has an input named "signalIn" and an output named "signalOut." To have a string of these stars in series, one would want the output of the first IIR star in the series to be connected to the input of the second star. And the output of the second star should be connected to the input of the third, etc. Thus, a Chain star that is a series of biquad filters would have an internal_map of
to specify that the output of one block is connected to the input of the next.
Another variant is the IfElse block. This star is just like Map, except that it has two possible replacement blocks. If the condition parameter is TRUE, then the true_block is used. Otherwise, the false_block is used. It is important to realize that the condition parameter is evaluated at preinitialization time. Once a replacement block has been selected, it cannot be changed. There are two uses for this block. It can be used to parameterize a galaxy in such a way that the parameter determines which of two functions is used within the computation. More interestingly, it can be used to implement statically-evaluated recursion.
Map star and its variants replace themselves with an instance of the block specified as the replacement block. What if that block is a galaxy within which the very Map star in question sits? This is a recursive reference to the galaxy, but a rather awkward one. In fact, in such a configuration, the preinitialization phase of execution will never terminate. The user has to manually abort such an execution in order to get it to terminate.
The IfElse star, however, can conditionally specify one of two replacement blocks. The condition parameter determines which block. One of the two replacement blocks can be a recursive reference to a galaxy as long as the condition parameter is modified. When the condition parameter changes state, going from TRUE to FALSE or FALSE to TRUE, then the choice of replacement block inside the new galaxy instance will change. This can be used to terminate the recursion.
Consider the example shown in figure 6-11.
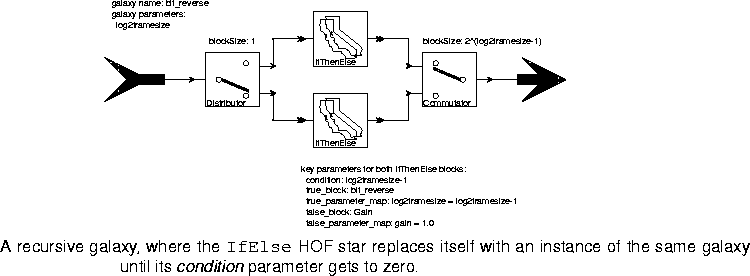
IfElse stars, each with a conditional recursive reference to the bit_reverse galaxy. The condition is log2framesize-1, and the log2framesize parameter for the inside instances of the galaxy is set to log2framesize-1. When log2framesize gets to zero, the replacement block becomes a Gain star with unity gain (which of course has no effect). This terminates the recursion.With log2framesize = 3, after the preinitialization phase, the topology of the galaxy will have become that shown in figure 6-12.
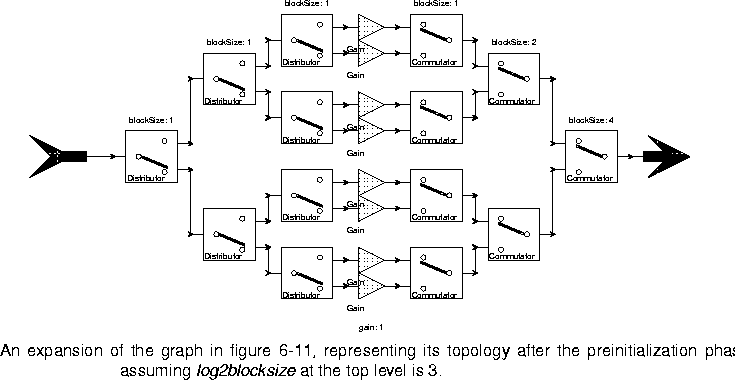
Distributors, Gains, and Commutators has no effect at all). Unfortunately, we currently have no mechanism for automatically displaying this expanded graph visually. It can, however, be examined using ptcl.
An example of the use of the BusSplit star is shown in figure
6-13.
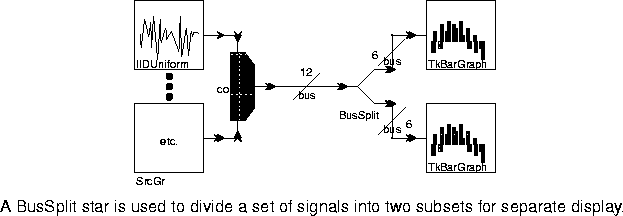
BusSplit star rewires the graph at preinitialization time and then self-destructs. Thus, it introduces zero run-time overhead.
Examples of the uses of Nop stars are shown in figure
6-14.
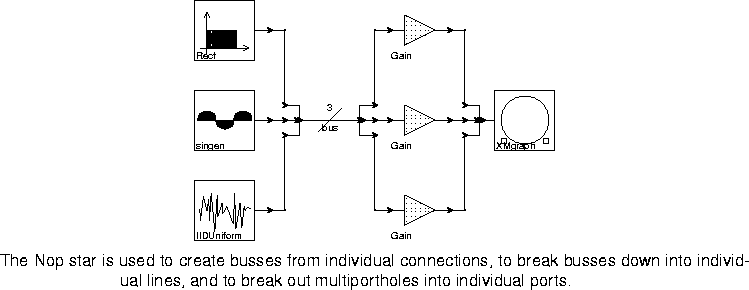
Nop star. The bus is then broken out into three individual lines, which are fed to three Gain stars. The most interesting use of the Nop star, however, is the one on the right. The XMgraph star shown there has a multiporthole input. The Nop star is simply deposited on top of the multiporthole to provide it with three individual inputs. Why do this? Because when connecting multiple signals to a multiporthole input, as done for example in figure
6-3, it is difficult to control which input line goes to which specific porthole in the multiporthole set. Putting the Nop star on the porthole gives us this control with no additional run-time cost.






Copyright © 1990-1997, University of California. All rights reserved.