





The HOF demos are divided by domain, and are accessed through the demo palette of the individual domain. As of this writing, only the SDF, DDF, DE, and CGC domains have HOF demo palettes.
The top-level demo palette for the HOF/SDF demos is shown in figure
6-17. The icon labeled "test" points to a set of demos that are not documented here and are used as part of the regression tests in Ptolemy.
The icon labeled "test" points to a set of demos that are not documented here and are used as part of the regression tests in Ptolemy.
addingSinWaves
This demo generates a number of sine waves given by the parameter number_of_sine_waves and adds them all together. The amplitude of each sine wave is controlled by a Tk slider that is inserted into the control panel when the system is run. The frequency in radians of each sine wave (relative to a sample rate of 2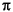 ) is instance_number multiplied by
) is instance_number multiplied by 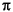 /32. Thus, the first sine wave will have a period of 64 samples. The second will have a period of 32. The third will have a period of 16, etc. The sum of these sine waves is displayed in bar-graph form.
/32. Thus, the first sine wave will have a period of 64 samples. The second will have a period of 32. The third will have a period of 16, etc. The sum of these sine waves is displayed in bar-graph form.
busManipulations
This demo is shown above in figure
fft
This system implements a recursive definition of a decimation-in-time fast Fourier transform, comparing its output against that of a direct implementation in C++. The system is configured to use 32 point FFTs to implement a 256 point FFT. The granularity is controllable with the parameters, and can be taken all the way down to the level of multipliers and adders. This system is discussed in detail in [Lee94].
fft2d
This system generates the same square as in the square demo, and then computes its two-dimensional FFT using the method given in figure
fourierSeries
This system generates a number of sinusoids as given by the number_of_terms parameter. These are then weighted by the appropriate Fourier series coefficients so that the sum of the sinusoids gives the finite Fourier series approximation for a square wave with period given by the period parameter.
fourierSeriesMma
This system is similar to the fourierSeries system above, but uses Mathematica to calculate parameter values. Mathematica must be licensed on the local workstation for this demo to run.
phased_array
This system models a planar array of sensors with beamforming and steering, such as might be used with a microphone array or a radar system. The sensors can be positioned arbitrarily in a plane. With the default parameters, 16 sensors are uniformly spaced along the vertical axis, half a wavelength apart, except for one, the fourth, which is offset along the horizontal axis by one tenth of a wavelength. The gain of the array as a function of direction is plotted in both polar and rectangular form (the latter in dB). A Hamming window is applied to the sensor data, as is a steering vector which directs the beam downwards. Zoom into the center of the polar plot to see the effect of the offset sensor. Try changing the parameter_map of the left-most MapGr higher-order function to realign the offset sensor, and observe the effect on the gain pattern.
RadarChainProcessing
This system simulates radar without beamforming. In this simulation, we simulate the effect of an electromagnetic signal traveling from a transmitter to targets and going back to receivers.The delay of the returned signal is used to provide information on the range of the target. The frequency shift, or Doppler effect, is used to provide information on the speed of the target. Thus, with these parameters, we estimate the target's properties as in a narrow band radar.
The system has been converted from a data parallel form that uses a five-dimensional data array to a functional parallel form that uses higher-order functions to produce streams of streams. The five dimensions are range bin, doppler filters, number of sensors, number of targets and number of pulses. For more information, see http://ptolemy.eecs.berkeley.edu/papers/Radarsimu.ps.Z.
sawtooth
This demo is shown above in figure
scramble
This system demonstrates the bit_reverse galaxy shown above in figure
square
This system demonstrates the BusMerge HOF star. It generates an image consisting of a light square on a dark background. The image is first represented using a bus, where each connection in the bus represents one row. The Commutator star then rasterizes the image.
wildColors
This demo is shown above in figure
At this time, there are only two simple demos in the DE domain.
poisson
This system generates any number of Poisson processes (default 10) and displays them together. To distinguish them, each process produces events with a distinct value.
exponential
Combine a number of Poisson processes and show that the interarrival times are exponentially distributed by plotting a histogram. Notice that the histogram bin centered at zero is actually only half as a wide as the others (since the interarrival time cannot be negative), so the histogram displays a value for the zero bin that is half as high as what would be expected.
The top-level demo palette for the HOF demos in the C Code generation domain (CGC) is shown in figure
6-18 .
.
busses
Create a set of ramps of different slopes and display them in both a bar chart and using pxgraph.
scrambledCGC
This system demonstrates recursion in code generation by taking a ramp in and reordering samples in bit-reversed order.
soundHOF
This system produces a sound made by adding a fundamental and its harmonics in amounts controlled by sliders. This demo will work only on Sun workstations.
wildColorsCGC
This system is a CGC version of the SDF demo wildColors. It creates a number of random sequences and plots them in a pair of bar graphs.
-







Copyright © 1990-1997, University of California. All rights
reserved.









 ) is instance_number multiplied by
) is instance_number multiplied by 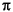 /32. Thus, the first sine wave will have a period of 64 samples. The second will have a period of 32. The third will have a period of 16, etc. The sum of these sine waves is displayed in bar-graph form.
/32. Thus, the first sine wave will have a period of 64 samples. The second will have a period of 32. The third will have a period of 16, etc. The sum of these sine waves is displayed in bar-graph form.