Page 20 out of 24 total pages
The distributed discrete event (DDE) model of computation incorporates a distributed notion of time into a dataflow style of communication. Time progresses in a DDE model when the actors in the model execute and communicate. Actors in a DDE model communicate by sending messages through bounded, FIFO channels. Time in a DDE model is distributed and localized, and the actors of a DDE model each maintain their own local notion of the current time. Local time information is shared between two connected actors whenever a communication between said actors occurs. Conversely, communication between two connected actors can occur only when constraints on the relative local time information of the actors are adhered to.
The DDE domain is based on distributed discrete event processing and leverages a wealth of research devoted to this topic. Several tutorial publications on this topic exist in [18][24][39][60]. The DDE domain implements a specific variant of distributed discrete event systems (DDES) as expounded by Chandy and Misra [18]. While the DDE domain has similarities with DDES, the distributed discrete event domain serves as a framework for studying DDES with two special emphases. First we consider DDES from a dataflow perspective; we view DDE as an implementation of the Kahn dataflow model [41] with distributed time added on top. Second we study DDES not with the goal of improving execution speed (as has been the case traditionally). Instead we study DDES to learn its usefulness in modeling and designing systems that are timed and distributed.
Operationally, the semantics of the DDE domain can be separated into two functionalities. The first functionality relates to how time advances during the communication of data and how communication proceeds via blocking reads and writes. The second functionality considers how a DDE model prevents deadlock due to local time dependencies. The technique for preventing deadlock involves the communication of null messages that consist solely of local time information.
A DDE model consists of a network of sequential actors that are connected via unidirectional, bounded, FIFO queues. Tokens are sent from a sending actor to a receiving actor by placing a token in the appropriate queue where the token is stored until the receiving actor consumes it. If a process attempts to read a token from a queue that is empty, then the process will block until a token becomes available on the channel. If a process attempts to write a token to a queue that is full, then the process will block until space becomes available for more tokens in that queue. Note that this blocking read/write paradigm is equivalent to the operational semantics found in non-timed process networks (PN) as implemented in Ptolemy II (see the PN Domain chapter).
If all processes in a DDE model simultaneously block, then the model deadlocks. Deadlock that is due to processes that are either waiting to read from an empty queue, read blocks, or waiting to write to a full queue, write blocks, then we say that the model has experienced non-timed deadlock. Non-timed deadlock is equivalent to the notion of deadlock found in bounded process networks scheduling problems as outlined by Parks [68]. If a non-timed deadlock is due to a model that consists solely of processes that are read blocked, then we say that a real deadlock has occurred and the model is terminated. If a non-timed deadlock is due to a model that consists of at least one process that is write blocked, then the capacity of the full queues are increased until deadlock no longer exists. Such deadlocks are called artificial deadlock, and the policy of increasing the capacity of full queues was shown by Parks to guarantee the execution of a model in bounded memory whenever possible.
Each actor in a DDE model maintains a local notion of time. As tokens are communicated between actors, time stamps are associated with each token. Whenever an actor consumes a token, the actor's current time is set to be equal to that of the consumed token's time stamp. The time stamp value applied to outgoing tokens of an actor is equivalent to that actor's output time. For actors that model a process in which there is delay between incoming time stamps and corresponding outgoing time stamps, then the output time is always greater than the current time; otherwise, the output time is equal to the current time. We refer to actors of the former case as delay actors.
For a given queue containing time stamped tokens, the time stamp of the first token currently contained by the queue is referred to as the receiver time of the queue. If a queue is empty, its receiver time is the value of the time stamp associated with the last token to flow through the queue, or 0.0 if no tokens have traveled through the queue. An actor may consume a token from an input queue given that the queue has a token available and the receiver time of the queue is less than the receiver times of all other input queues contained by the actor. If the queue with the smallest receiver time is empty, then the actor blocks until this queue receives a token, at which time the actor considers the updated receiver time in selecting a queue to read from.
Figure 15.1 shows three actors, each with three input queues. Actor A has two tokens available on the top queue, no tokens available on the middle queue and one token available on the bottom queue. The receiver times of the top, middle and bottom queue are respectively, 17.0, 12.0 and 15.0. Since the queue with the minimum receiver time (the middle queue) is empty, A must block on this queue before it proceeds. In the case of actor B, the minimum receiver time belongs to the bottom queue. Thus, B would proceed by consuming the token found on the bottom queue. After consuming this token, B would then compare all of its receiver times to determine which token it could consume from next. Actor C is an example of an actor that contains multiple input queues with identical receiver times. To accommodate this situation, each actor assigns a unique priority to each input queue. An actor can consume a token from a queue if no other queue has a lower receiver time and if all queues that have an identical receiver time also have a lower priority.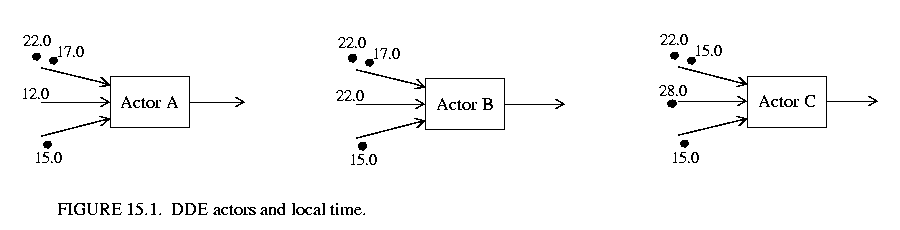
Each receiver has a completion time that is set during the initialization of a model. The completion time of the receiver specifies the time after which the receiver will no longer operate. If the time stamp of the oldest token in a receiver exceeds the completion time, then that receiver will become inactive.
Deadlocks can occur in a DDE model in a form that differs from the deadlocks described in the previous section. This alternative form of deadlock occurs when an actor read blocks on an input port even though it contains other ports with tokens. The topology of a DDE model can lead to deadlock as read blocked actors wait on each other for time stamped tokens that will never appear. Figure 15.2 illustrates this problem. In this topology, consider a situation in which actor A only creates tokens on its lower output queue. This will lead to tokens being created on actor C's output queue but no tokens will be created on B's output queue (since B has no tokens to consume). This situation results in D read blocking indefinitely on its upper input queue even though it is clear that no tokens will ever flow through this queue. The result: timed deadlock! The situation shown in figure 15.2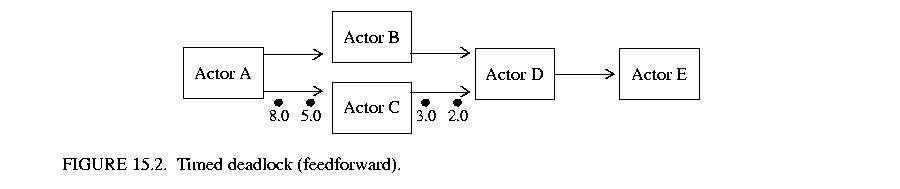
is only one example of timed deadlock. In fact there are two types of timed deadlock: feedforward and feedback.
Figure 15.2 is an example of feedforward deadlock. Feedforward deadlock occurs when a set of connected actors are deadlocked such that all actors in the set are read blocked and at least one of the actors in the set is read blocked on an input queue that has a receiver time that is less than the local clock of the input queue's source actor. In the example shown above, the upper input queue of B has a receiver time of 0.0 even though the local clock of A has advanced to 8.0.
Feedback deadlock occurs when a set of cyclically connected actors are deadlocked such that all actors in the set are read blocked and at least one actor in the set, say actor X, is read blocked on an input queue that can read tokens which are directly or indirectly a result of output from that same actor (actor X). Figure 15.3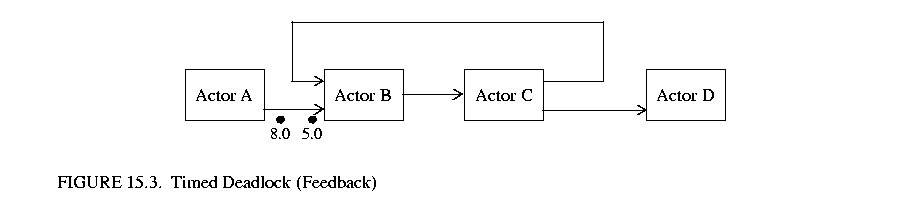
is an example of feedback timed deadlock. Note that B can not produce an output based on the consumption of the token timestamped at 5.0 because it must wait for a token on the upper input that depends on the output of B!
To address feedforward timed deadlock, null tokens are employed. A null token provides an actor with a means of communicating time advancement even though data (real tokens) are not being transmitted. Whenever an actor consumes a token, it places a null token on each of its output queues such that the time stamp of the null token is equal to the current time of the actor. Thus, if actor A of figure 15.2, produced a token on its lower output queue at time 5.0, it would also produce a null token on its upper output queue at time 5.0.
If an actor encounters a null token on one of its input queues, then the actor does the following. First it consumes the tokens of all other input queues it contains given that the other input queues have receiver times that are less than or equal to the time stamp of the null token. Next the actor removes the null token from the input queue, sets its current time to equal the time stamp of the null token and produces a null token on all output queues such that the produced null tokens are time stamped to the current time. As an example, if B in figure 15.2 consumes a null token on its input with a time stamp of 5.0 then it would also produce a null token on its output with a time stamp of 5.0.
The result of using null tokens is that time information is evenly propagated through a model's topology. The beauty of null tokens is that they inform actors of inactivity in other components of a model without requiring centralized dissemination of this information. Given the use of null tokens, feedforward timed deadlock is prevented in the execution of DDE models. It is important to recognize that null tokens are used solely for the purpose of avoiding deadlocks. Null tokens do not represent any actual components of the physical system being modeled. Hence, we do not think of a null token as a real token. Furthermore, the production of a null token that is the direct result of the consumption of a null token is not considered computation from the standpoint of the system being modeled. The idea of null tokens was first espoused by Chandy and Misra [18].
We address feedback timed deadlock as follows. All feedback loops are required to have a cumulative time stamp increment that is greater than zero. In other words, feedback loops are required to contain delay actors. Peacock, Wong and Manning [69] have shown that a necessary condition for feedback timed deadlock is that a feedback loop must contain no delay actors. The delay value (delay = output time - current time) of a delay actor must be chosen wisely; it must be less then the smallest delta time of all other actors contained in the same feedback loop. Delta time is the difference between the time stamps of a token that is consumed by an actor and the corresponding token that is produced in direct response. If a system being modeled has characteristics that prevent a fixed, positive lower bound on delta time from being specified, then our approach can not solve feedback timed deadlock. Such a situation is referred to as a Zeno condition. An application involving an approximated Zeno condition is discussed in section 15.3 below.
The DDE software architecture provides one delay actor for use in preventing feedback timed deadlock: FBDelay. We have left out a key operational detail of FBDelay that relates to the process of initializing execution in a model with a feedback delay. This discussion can be found in section 15.4.3 below.
The field of distributed discrete event simulation, also referred to as parallel discrete event simulation (PDES), has been an active area of research since the late 1970's [18][24][39][60][69]. Recently there has been a resurgence of activity [5][6][10]. This is due in part to the wide availability of distributed frameworks for hosting simulations and the application of parallel simulation techniques to non-research oriented domains. For example, several WWW search engines are based on network of workstation technology.
The field of distributed discrete event simulation can be cast into two camps that are distinguished by the blocking read approach taken by the actors. One camp was introduced by Chandy and Misra [18][24][60][69] and is known as conservative blocking. The second camp was introduced by David Jefferson through the Jet Propulsion Laboratory Time Warp system and is referred to as the optimistic approach [39][24]. The implementation found in the DDE domain follows the conservative approach.
To illustrate distributed discrete event execution, we have developed an applet that features a feedback topology and incorporates polymorphic as well as DDE specific actors. The model, shown in figure 15.4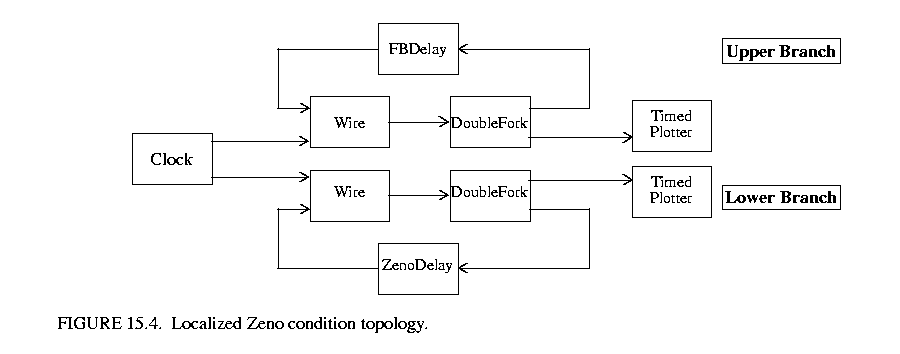
, consists of a single source actor (ptolemy/actor/lib/Clock) and an upper and lower branch of four actors each. The upper and lower branches have identical topologies and are fed an identical stream of tokens from the Clock source with the exception that in the lower branch ZenoDelay replaces FBDelay.
As with all feedback topologies in DDE (and DE) models, a positive time delay is necessary in feedback loops to prevent deadlock. If the time delay of a given loop is lower bounded by zero but can not be guaranteed to be greater than a fixed positive value, then a Zeno condition occurs in which time will not advance beyond a certain point even though the actors of the feedback loop continue to execute without deadlocking. ZenoDelay extends FBDelay and is designed so that a Zeno condition will be encountered. When execution of the model begins, both FBDelay and ZenoDelay are used to feed back null tokens into Wire so that the model does not deadlock. After local time exceeds a preset value, ZenoDelay reduces its delay so that the lower branch approximates a Zeno condition.
In centralized discrete event systems, Zeno conditions prevent progress in the entire model. This is true because the feedback cycle experiencing the Zeno condition prevents time from advancing in the entire model. In contrast, distributed discrete event systems localize Zeno conditions as much as is possible based on the topology of the system. Thus, a Zeno condition can exist in the lower branch and the upper branch will continue its execution unimpeded. Localizing Zeno conditions can be useful in large scale modeling in which a Zeno condition may not be discovered until a great deal of time has been invested in execution of the model. In such situations, partial data collection may proceed prior to correction of the delay error that resulted in the Zeno condition.
To build a DDE application, a DDEDirector must be used. This will ensure that each actor under control of the director will be allocated DDEReceivers and that each actor will be assigned a TimeKeeper to manage the actor's local notion of time. The DDE domain is typed so that actors used in a model must be derived from ptolemy/actor/TypedAtomicActor. The DDE domain is designed to use both DDE specific actors as well as polymorphic actors. DDE specific actors can take advantage of DDEActor and DDEIOPort which are designed to provide convenient support for specifying time in the production and consumption of tokens.
The DDE model of computation makes one very strong assumption about the execution of an actor: all input ports of an actor operating in a DDE model must be regularly polled to determine which input channel has the oldest pending event. Any actor that adheres to this assumption can operate in a DDE model. Thus, many polymorphic actors found in ptolemy/actor/[lib, gui] are suitable for operation in DDE models. For convenience, DDEActor was developed to simplify the construction of actors that have DDE semantics. DDEActor has three key methods as follows:
This method returns the actor thread's local notion of time. This method relies on Java's Thread.currentThread() returning the thread that is assigned to the actor and hence this method is intended for self-referencing. If actor A calls getCurrentTime() of actor B, then the result will be the current time of A (not B as one might expect).
This method polls each input port of an actor and returns the (non-Null) token that represents the oldest event. This method blocks accordingly as outlined in section 15.2.1 (Communicating Time).
This method returns the input IOPort from which the last (non-Null) token was consumed. This method presumes that getNextToken() is being used for token consumption.
DDEIOPort extends TypedIOPort with parameters for specifying time stamp values of tokens that are being sent to neighboring actors. Since DDEIOPort extends TypedIOPort, use of DDEIOPorts will not violate the type resolution process. DDEIOPort is not necessary to facilitate communication between actors executing in a DDE model; standard TypedIOPorts are sufficient in most communication. DDEIOPorts become useful when the time stamp to be associated with an outgoing token is greater than the current time of the sending actor. Hence, DDEIOPorts are only useful in conjunction with delay actors (see "Enabling Communication: Advancing Time" on page 15-2, for a definition of delay actor). Most polymorphic actors available for Ptolemy II are not delay actors.
In order to execute feedback topologies that will not deadlock, FBDelay actors must be used. FBDelay is found in the DDE kernel package. FBDelay actors do not perform computation, but instead increment the time stamps of tokens that flow through them by a specified delay. The delay value of an FBDelay actor must be chosen to be less than the delta time of the feedback cycle in which the FBDelay actor is contained. Elaborate delay values can be specified by overriding the getDelay() method in subclasses of FBDelay. An example of such can be found in ptolemy/domains/dde/demo/LocalZeno/ZenoDelay.java.
A difficulty found in feedback cycles occurs in the initialization of a model's execution. In figure 15.5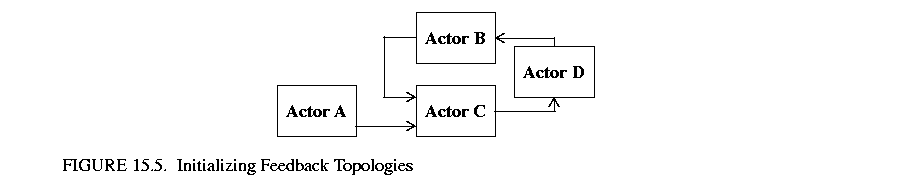
we see that even if Actor B is an FBDelay actor, the system will deadlock if the first event is created by A since C will block on an event from B. To alleviate this problem a special time stamp value has been reserved: TimeQueuedReceiver.IGNORE. When an actor encounters an event with a time stamp of IGNORE (an ignore event), the actor will ignore the event and the input channel it is associated with. The actor then considers the other input channels in determining the next available event. After a non-ignore event is encountered and consumed by the actor, all ignore events will be cleared. If all of an actor's input channels contain ignore events, then the actor will clear all ignore events and then proceed with normal operation.
The initialize method of FBDelay produces an ignore event. Thus, in figure 15.5, if B is an FBDelay actor, the ignore event it produces will be sent to C's upper input channel allowing C to consume the first event of A. The production of null tokens and feedback delays will then be sufficient to continue execution from that point on. Note that the production of an ignore event by a FBDelay actor serves as a major distinction between it and all other actors. If a delay is desired simply to represent the computational delay of a given model, an FBDelay actor should not be used.
The intricate operation of ignore events requires special consideration when determining the positioning of an FBDelay actor in a feedback topology. An FBDelay actor should be placed so that the ignore event it produces will be ignored in deference to the first real event that enters a feedback cycle. Thus, choosing actor D as an FBDelay actor in figure 15.5 would not be useful given that the first real event entering the cycle is created by A.
For a model to have DDE semantics, it must have a DDEDirector controlling it. This ensures that the receivers in the ports are DDEReceivers. As with all process domains, each actor in a DDE model is under the control of a ProcessThread, or in the case of DDE, a DDEThread. DDEThreads contain a TimeKeeper that manages the local notion of time that is associated with the DDEThread's actor.
The UML diagram of the local time management system of the DDE domain is shown in figure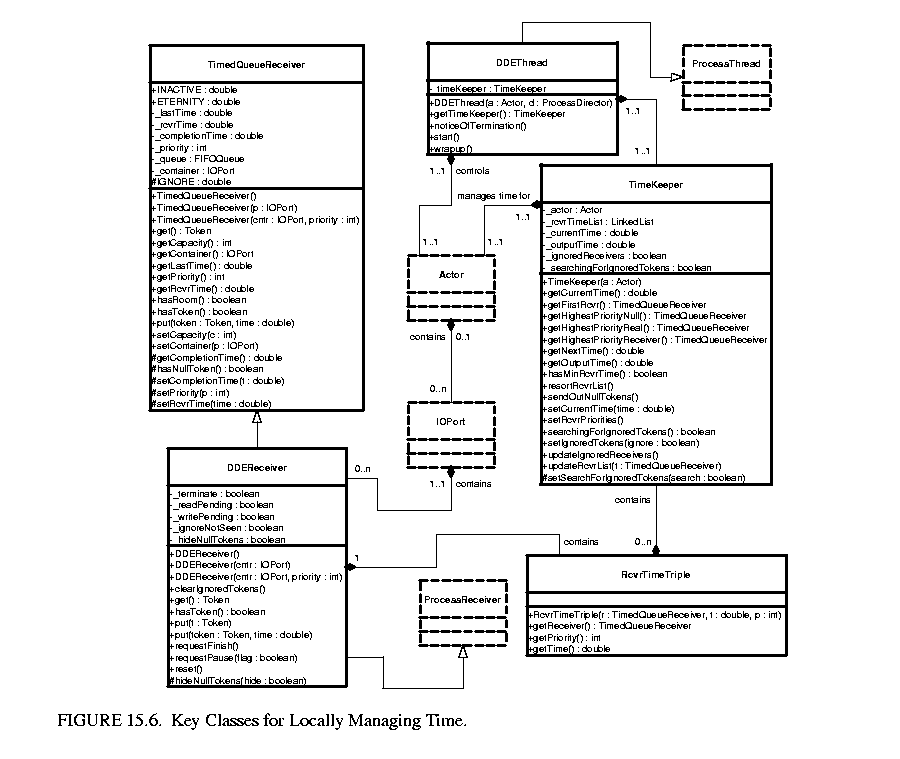
15.6 and consists of TimedQueueReceiver, DDEReceiver, DDEThread and TimeKeeper. Since time is localized, the DDEDirector does not have a direct role in this process. Note that DDEReceiver is derived from TimedQueueReceiver. The primary purpose of TimedQueueReceiver is to keep track of a receiver's local time information. DDEReceiver adds blocking read/write functionality to TimedQueueReceiver.
When a DDEDirector is initialized, it instantiates a DDEThread for each actor that the director manages. DDEThreads are derived from ProcessThreads. ProcessThreads provide functionality that is common to all of the process domains (e.g., CSP, DDE and PN). The directors of all process domains (including DDE) assign a single actor to each ProcessThread. ProcessThreads take responsibility of their assigned actor's execution by invoking the iteration methods of the actor. The iteration methods are prefire(), fire() and postfire(); ProcessThreads also invoke wrapup() on the actors they control.
DDEThread extends the functionality of ProcessThread. Upon instantiation, a DDEThread creates a TimeKeeper object and assigns this object to the actor that it controls. The TimeKeeper gets access to each of the DDEReceivers that the actor contains. Each of the receivers can access the TimeKeeper and through the TimeKeeper the receivers can then determine their relative receiver times. With this information, the receivers are fully equipped to apply the appropriate blocking rules as they get and put time stamped tokens.
DDEReceivers use a dynamic approach to accessing the DDEThread and TimeKeeper. To ensure domain polymorphism, actors (DDE or otherwise) do not have static references to the TimeKeeper and DDEThread that they are controlled by. To ensure simplified mutability support, DDEReceivers do not have a static reference to TimeKeepers. Access to the local time management facilities is accomplished via the Java Thread.currentThread() method. Using this method, a DDEReceiver dynamically accesses the thread responsible for invoking it. Presumably the calling thread is a DDEThread and appropriate steps are taken if it is not. Once the DDEThread is accessed, the corresponding TimeKeeper can be accessed as well. The DDE domain uses this approach to great gain in DDEReceiver.put(Token) and DDEReceiver.get().
DDEReceiver.put(Token) is derived from the Receiver interface and is accessible by all actors and domains. To facilitate local time advancement, DDEReceiver has a second put() method that has a time argument: DDEReceiver.put(Token, double). This second DDE-specific version of put() is taken advantage of without extensive code by using Thread.currentThread(). DDEReceiver.put() is shown below:
public void put(Token token)1 {
Thread thread = Thread.current-
Thread();
double time = getLastTime();
if( thread instanceof DDEThread ) {
TimeKeeper timeKeeper = ((DDETh-
read)thread).getTimeKeeper();
time = timeKeeper.getOutputTime();
}
put( token, time )2;
}
Similar uses of Thread.currentThread() are found throughout DDEReceiver and DDEDirector. Note that while Thread.currentThread() can be quite advantageous, it means that if particular code is called by an inappropriate thread, problems may occur. Such an issue makes testing of code difficult.
The other kernel classes of the DDE domain are shown in figure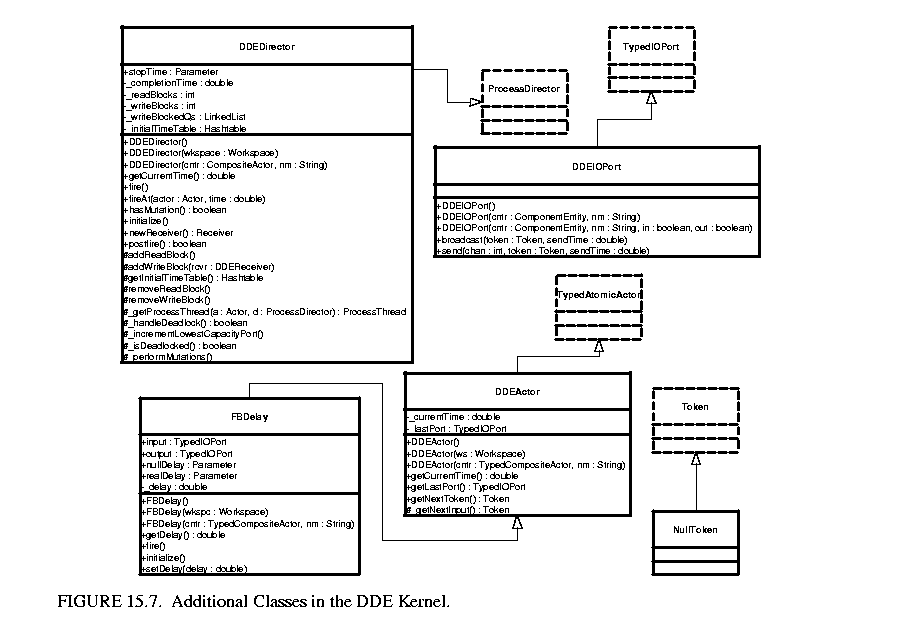 
15.7. The purpose of the DDEDirector is to detect and (if possible) resolve timed and/or non-timed deadlock of the model it controls. Whenever a receiver blocks, it informs the director. The director keeps track of the number of active processes, and the number of processes that are either blocked on a read or write. Artificial deadlocks are resolved by increasing the queue capacity of write-blocked receivers.
Execution of a model ends if either an unresolvable deadlock occurs, the director's completion time is exceeded by all of the actors it manages, or early termination is requested (e.g., by a user interface button). The director's completion time is set via the public stopTime parameter of DDEDirector. The completion time is passed on to each DDEReceiver. If a receiver's receiver time exceeds the completion time, then the receiver becomes inactive. If all receivers of an actor become inactive and the actor is not a source actor, then the actor will end execution and its wrapup() method will be called. In such a scenario, the actor is said to have terminated normally.
Early terminations and unresolvable deadlocks share a common mechanism for ending execution. Each DDEReceiver has a boolean _terminate flag. If the flag is set to true, then the receiver will throw a TerminateProcessException the next time any of its methods are invoked. TerminateProcessExceptions are part of the ptolemy/actor/process package and ProcessThreads know to end an actor's execution if this exception is caught. In the case of unresolvable deadlock, the _terminate flag of all blocked receivers is set to true. The receivers are then awakened from blocking and they each throw the exception.
Previously we have discussed in great detail the notion of timed and non-timed deadlock. Separate from these notions is a different kind of deadlock that can be inherent in a modeling environment if the environment is not designed properly. This notion of deadlock can occur if a system is not thread safe. Given the extensive use of Java threads throughout Ptolemy II, great care has been taken to ensure thread safety; we want no bugs to exist that might lead to deadlock based on the structure of the Ptolemy II modeling environment. Ptolemy II uses monitors to guarantee thread safety. A monitor is a method for ensuring mutual exclusion between threads that both have access to a given portion of code. To ensure mutual exclusion, threads must acquire a monitor (or lock) in order to access a given portion of code. While a thread owns a lock, no other threads can access the corresponding code.
There are several objects that serve as locks in Ptolemy II. In the process domains, there are four primary objects upon which locking occurs: Workspace, ProcessReceiver, ProcessDirector and AtomicActor. The danger of having multiple locks is that separate threads can acquire the locks in competing orders and this can lead to deadlock. A simple illustration is shown in figure 15.8. Assume that both lock A and lock B are necessary to perform a given set of operations and that both thread 1 and thread 2 want to perform the operations. If thread 1 acquires A and then attempts to acquire B while thread 2 does the reverse, then deadlock will occur.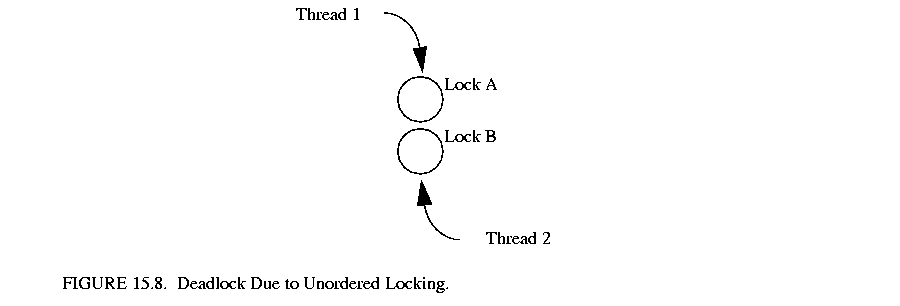 
There are several ways to avoid the above problem. One technique is to combine locks so that large sets of operations become atomic. Unfortunately this approach is in direct conflict with the whole purpose behind multi-threading. As larger and larger sets of operations utilize a single lock, the limit of the corresponding concurrent program is a sequential program!
Another approach is to adhere to a hierarchy of locks. A hierarchy of locks is an agreed upon order in which locks are acquired. In the above case, it may be enforced that lock A is always acquired before lock B. A hierarchy of locks will guarantee thread safety [43].
The process domains have an unenforced hierarchy of locks. It is strongly suggested that users of Ptolemy II process domains adhere to this suggested locking hierarchy. The hierarchy specifies that locks be acquired in the following order: 
The way to apply this rule is to prevent synchronized code in any of the above objects from making a call to code that is to the left of the object in question.