Page 19 out of 24 total pages
The communicating sequential processes (CSP) domain in Ptolemy II models a system as a network of sequential processes that communicate by passing messages synchronously through channels. If a process is ready to send a message, it blocks until the receiving process is ready to accept the message. Similarly if a process is ready to accept a message, it blocks until the sending process is ready to send the message. This model of computation is non-deterministic as a process can be blocked waiting to send or receive on any number of channels. It is also highly concurrent.
The CSP domain is based on the model of computation (MoC) first proposed by Hoare [36][37] in 1978. In this MoC, a system is modeled as a network of processes communicate solely by passing messages through unidirectional channels. The transfer of messages between processes is via rendezvous, which means both the sending and receiving of messages from a channel are blocking: i.e. the sending or receiving process stalls until the message is transferred. Some of the notation used here is borrowed from Gregory Andrews' book on concurrent programming [4], which refers to rendezvous-based message passing as synchronous message passing.
Applications for the CSP domain include resource management and high level system modeling early in the design cycle. Resource management is often required when modeling embedded systems, and to further support this, a notion of time has been added to the model of computation used in the domain. This differentiates our CSP model from those more commonly encountered, which do not typically have any notion of time, although several versions of timed CSP have been proposed [34]. It might thus be more accurate to refer to the domain using our model of computation as the "Timed CSP" domain, but since the domain can be used with and without time, it is simply referred to as the CSP domain.
At the core of CSP communication semantics are two fundamental ideas. First is the notion of atomic communication and second is the notion of nondeterministic choice. It is worth mentioning a related model of computation known as the calculus of communicating systems (CCS) that was independently developed by Robin Milner in 1980 [58]. The communication semantics of CSP are identical to those of CCS.
Atomic communication is carried out via rendezvous and implies that the sending and receiving of a message occur simultaneously. During rendezvous both the sending and receiving processes block until the other side is ready to communicate; the act of sending and receiving are indistinguishable activities since one can not happen without the other. A real world analogy to rendezvous can be found in telephone communications (without answering machines). Both the caller and callee must be simultaneously present for a phone conversation to occur. Figure 14.1 shows the case where one process is ready to send before the other process is ready to receive. The communication of information in this way can be viewed as a distributed assignment statement.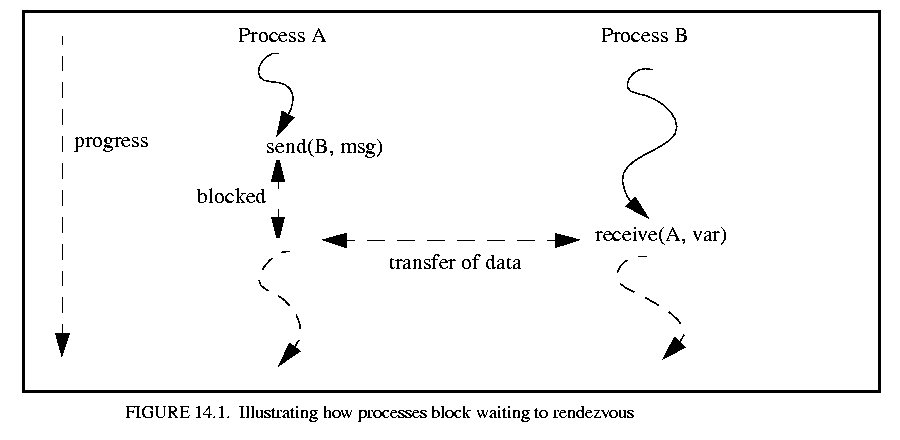
The sending process places some data in the message that it wants to send. The receiving process assigns the data in the message to a local variable. Of course, the receiving process may decide to ignore the contents of the message and only concern itself with the fact that a message arrived.
Nondeterministic choice provides processes with the ability to randomly select between a set of possible atomic communications. We refer to this ability as nondeterministic rendezvous and herein lies much of the expressiveness of the CSP model of computation. The CSP domain implements nondeterministic rendezvous via guarded communication statements. A guarded communication statement has the form
guard; communication => statements;
The guard is only allowed to reference local variables, and its evaluation cannot change the state of the process. For example it is not allowed to assign to variables, only reference them. The communication must be a simple send or receive, i.e. another conditional communication statement cannot be placed here. Statements can contain any arbitrary sequence of statements, including more conditional communications.
If the guard is false, then the communication is not attempted and the statements are not executed. If the guard is true, then the communication is attempted, and if it succeeds, the following statements are executed. The guard may be omitted, in which case it is assumed to be true.
There are two conditional communication constructs built upon the guarded communication statements: CIF and CDO. These are analogous to the if and while statements in most programming languages. They should be read as "conditional if" and "conditional do". Note that each guarded communication statement represents one branch of the CIF or CDO. The communication statement in each branch can be either a send or a receive, and they can be mixed freely.
For each branch in the CIF, the guard (G1, G2,...) is evaluated. If it is true (or absent, which implies true), then the associated communication statement is enabled. If one or more branch is enabled, then the entire construct blocks until one of the communications succeeds. If more than one branch is enabled, the choice of which enabled branch succeeds with its communication is made nondeterministically. Once the successful communication is carried out, the associated statements are executed and the process continues. If all of the guards are false, then the process continues executing statements after the end of the CIF.
It is important to note that, although this construct is analogous to the common if programming construct, its behavior is very different. In particular all guards of the branches are evaluated concurrently, and the choice of which one succeeds does not depend on its position in the construct. The notation "[]" is used to hint at the parallelism in the evaluation of the guards. In a common if, the branches are evaluated sequentially and the first branch that is evaluated to true is executed. The CIF construct also depends on the semantics of the communication between processes, and can thus stall the progress of the thread if none of the enabled branches is able to rendezvous.
The behavior of the CDO is similar to the CIF in that for each branch the guard is evaluated and the choice of which enabled communication to make is taken nondeterministically. However the CDO repeats the process of evaluating and executing the branches until all the guards return false. When this happens the process continues executing statements after the CDO construct.
An example use of a CDO is in a buffer process which can both accept and send messages, but has to be ready to do both at any stage. The code for this would look similar to that in figure 14.2.
Note that in this case both guards can never be simultaneously false so this process will execute the CDO forever.
A deadlock situation is one in which none of the processes can make progress: they are all either blocked trying to rendezvous or they are delayed (see the next section). Thus two types of deadlock can be distinguished:
real deadlock - all active processes are blocked trying to communicate
time deadlock - all active processes are either blocked trying to communicate or are delayed, and at least one processes is delayed.
In the CSP domain, time is centralized. That is, all processes in a model share the same time, referred to as the current model time. Each process can only choose to delay itself for some period relative to the current model time, or a process can wait for time deadlock to occur at the current model time. In both cases, a process is said to be delayed.
When a process delays itself for some length of time from the current model time, it is suspended until time has sufficiently advanced, at which stage it wakes up and continues. If the process delays itself for zero time, this will have no effect and the process will continue executing.
A process can also choose to delay its execution until the next occasion a time deadlock is reached. The process resumes at the same model time at which it delayed, and this is useful as a model can have several sequences of actions at the same model time. The next occasion time deadlock is reached, any processes delayed in this manner will continue, and time will not be advanced. An example of using time in this manner can be found in section 14.3.2.
Time may be advanced when all the processes are delayed or are blocked trying to rendezvous, and at least one process is delayed. If one or more processes are delaying until a time deadlock occurs, these processes are woken up and time is not advanced. Otherwise, the current model time is advanced just enough to wake up at least one process. Note that there is a semantic difference between a process delaying for zero time, which will have no effect, and a process delaying until the next occasion a time deadlock is reached.
Note also that time, as perceived by a single process, cannot change during its normal execution; only at rendezvous points or when the process delays can time change. A process can be aware of the centralized time, but it cannot influence the current model time except by delaying itself. The choice for modeling time was in part influenced by Pamela [27], a run time library that is used to model parallel programs.
The model of computation used by the CSP domain differs from the original CSP [36] model in two ways. First, a notion of time has been added. The original proposal had no notion of time, although there have been several proposals for timed CSP [34]. Second, as mentioned in section 14.2.2, it is possible to use both send and receive in guarded communication statements. The original model only allowed receives to appear in these statements, though Hoare subsequently extended their scope to allow both communication primitives [37].
One final thing to note is that in much of the CSP literature, send is denoted using a "!", pronounced "bang", and receive is denoted using a "?", pronounced "query". This syntax was what was used in the original CSP paper by Hoare. For example, the languages Occam [14] and Lotos [21] both follow this syntax. In the CSP domain in Ptolemy II we use send and get, the choice of which is influenced by the desire to maintain uniformity of syntax across domains in Ptolemy II that use message passing. This supports the heterogeneity principle in Ptolemy II which enables the construction and interoperability of executable models that are built under a variety of models of computation. Similarly, the notation used in the CSP domain for conditional communication constructs differs from that commonly found in the CSP literature.
Several example applications have been developed which serve to illustrate the modeling capabilities of the CSP model of computation in Ptolemy II. Each demonstration incorporates several features of CSP and the general Ptolemy II framework. Below, four demonstrations have been selected that each emphasize particular semantic capabilities over others. The applications are described here, but not the code. See the directory $PTII/ptolemy/domains/csp/demo for the code.
The first demonstration, dining philosophers, serves as a natural example of core CSP communication semantics. This demonstration models nondeterministic resource contention, e.g., five philosophers randomly accessing chopstick resources. Nondeterministic rendezvous serves as a natural modeling tool for this example. The second example, hardware bus contention, models deterministic resource contention in the context of time. As will be shown, the determinacy of this demonstration constrains the natural nondeterminacy of the CSP semantics and results in difficulties. Fortunately these difficulties can be smoothly circumvented by the timing model that has been integrated into the CSP domain. The third demonstration, sieve of Eratosthenes, serves to demonstrate the mutability that is possible in CSP models. In this demonstration, the topology of the model changes during execution. The final demonstration, M/M/1 queue, features the pause/resume mechanism of Ptolemy II that can be used to control the progression of a model's execution in the CSP domain.
This implementation of the dining philosophers problem illustrates both time and conditional communication in the CSP domain. Five philosophers are seated at a table with a large bowl of food in the middle. Between each pair of philosophers is one chopstick, and to eat, a philosopher needs both the chopsticks beside him. Each philosopher spends his life in the following cycle: thinks for a while, gets hungry, picks up one of the chopsticks beside him, then the other, eats for a while and puts the chopsticks down on the table again. If a philosopher tries to grab a chopstick but it is already being used by another philosopher, then the philosopher waits until that chopstick becomes available. This implies that no neighboring philosophers can eat at the same time and at most two philosophers can eat at a time.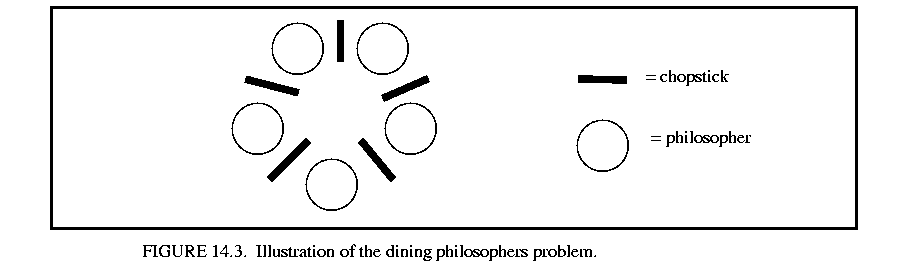 
The Dining Philosophers problem was first dreamt up by Edsger W. Dijkstra in 1965. It is a classic concurrent programming problem that illustrates the two basic properties of concurrent programming:
Liveness. How can we design the program to avoid deadlock, where none of the philosophers can make progress because each is waiting for someone else to do something?
Fairness. How can we design the program to avoid starvation, where one of the philosophers could make progress but does not because others always go first?
This implementation uses an algorithm that lets each philosopher randomly chose which chopstick to pick up first (via a CDO), and all philosophers eat and think at the same rates. Each philosopher and each chopstick is represented by a separate process. Each chopstick has to be ready to be used by either philosopher beside it at any time, hence the use of a CDO. After it is grabbed, it blocks waiting for a message from the philosopher that is using it. After a philosopher grabs both the chopsticks next to him, he eats for a random time. This is represented by calling delay() with the random interval to eat for. The same approach is used when a philosopher is thinking. Note that because messages are passed by rendezvous, the blocking of a philosopher when it cannot obtain a chopstick is obtained for free.
This algorithm is fair, as any time a chopstick is not being used, and both philosophers try to use it, they both have an equal chance of succeeding. However this algorithm does not guarantee the absence of deadlock, and if it is let run long enough this will eventually occur. The probability that deadlock occurs sooner increases as the thinking times are decreased relative to the eating times.
This demonstration consists of a controller, N processors and a memory block. At randomly selected points in time, each processor requests permission from the controller to access the memory block. The processors each have priorities associated with them and in cases where there is a simultaneous memory access request, the controller grants permission to the processor with the highest priority. Due to the atomic nature of rendezvous, it is impossible for the controller to check priorities of incoming requests at the same time that requests are occurring. To overcome this difficulty, an alarm is employed. The alarm is started by the controller immediately following the first request for memory access at a given instant in time. It is awakened when a delay block occurs to indicate to the controller that no more memory requests will occur at the given point in time. Hence, the alarm uses CSP's notion of delay blocking to make determ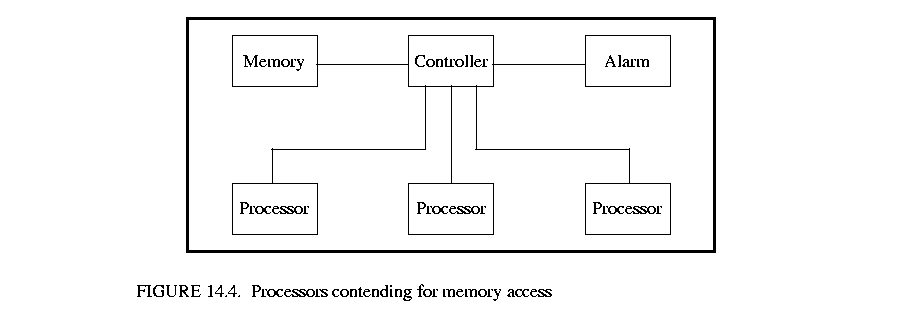
inistic an inherently non-deterministic activity.
This example implements the sieve of Eratosthenes. This is an algorithm for generating a list of prime numbers, illustrated in figure 14.5. It originally consists of a source generating integers, and one sieve filtering out all multiples of two. When the end sieve sees a number that it cannot filter, it creates a new sieve to filter out all multiples of that number. Thus after the sieve filtering out multiples of two sees the number three, it creates a new sieve that filters out multiples of three. This then continues with the three sieve eventually creating a sieve to filter out all multiples of five, and so on. Thus after a while there will be a chain of sieves each filtering out a different prime number. If any number passes through all the sieves and reaches the end with no sieve waiting, it must be another prime and so a new sieve is created for it.
This demo is an example of how changes to the topology can be made in the CSP domain. Each topology change here involves creating a new CSPSieve actor and connecting it to the end of the chain of sieves.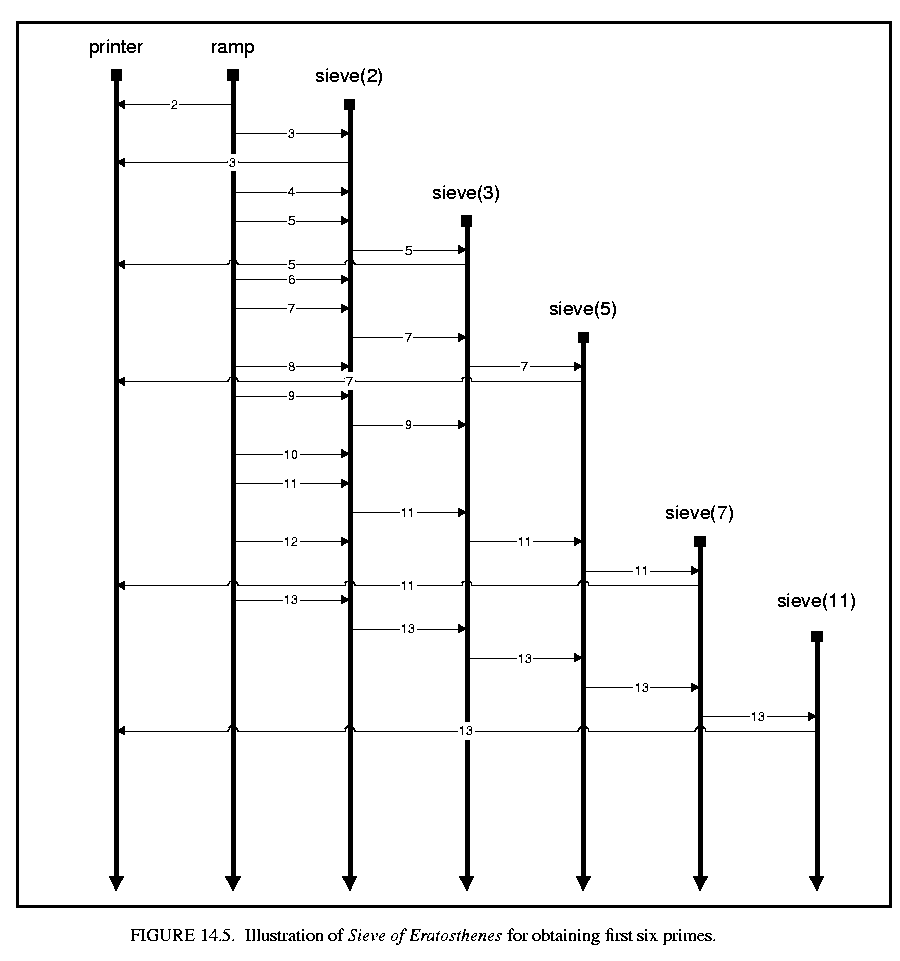
The example in figure 14.6 illustrates a simple M/M/1 queue. It has three actors, one representing the arrival of customers, one for the queue holding customers that have arrived and have not yet been served, and the third representing the server. Both the inter-arrival times of customers and the service times at the server are exponentially distributed, which of course is what makes this an M/M/1 queue.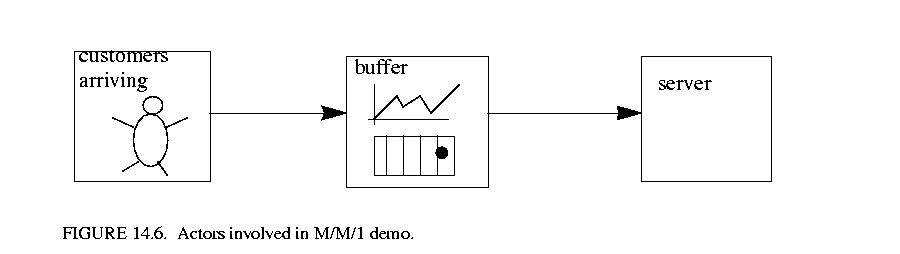 
This demo makes use of basic rendezvous, conditional rendezvous and time. By varying the rates for the customer arrivals and service times, and varying the length of the buffer, you can see various trade-offs. For example if the buffer length is too short, customers may arrive that cannot be stored and so are missed. Similarly if the service rate is faster than the customer arrival rate, then the server could spend a lot of time idle.
Another example demonstrates how pausing and resumption works. The setup is exactly the same as in the M/M/1 demo, except that the thread executing the model calls pause() on the director as soon as the model starts executing. It then waits two seconds, as arbitrary choice, and then calls resume(). The purpose of this demo is to show that the pausing and resuming of a model does not affect the model results, only its rate of progress. The ability to pause and resume a model is primarily intended for the user interface.
For a model to have CSP semantics, it must have a CSPDirector controlling it. This ensures that the receivers in the ports are CSPReceivers, so that all communication of messages between processes is via rendezvous. Note that each actor in the CompositeActor under the control of the CSPDirector represents a separate process in the model.
Since the ports contain CSPReceivers, the basic communication statements send() and get() will have rendezvous semantics. Thus the fact that a rendezvous is occurring on every communication is transparent to the actor code.
In order to use the conditional communication constructs, an actor must be derived from CSPActor. There are three steps involved:
1) Create a ConditionalReceive or ConditionalSend branch for each guarded communication statement, depending on the communication. Pass each branch a unique integer identifier, starting from zero, when creating it. The identifiers only need to be unique within the scope of that CDO or CIF.
2) Pass the branches to the chooseBranch() method in CSPActor. This method evaluates the guards, and decides which branch gets to rendezvous, performs the rendezvous and returns the identification number of the branch that succeeded. If all of the guards were false, -1 is returned.
3) Execute the statements for the guarded communication that succeeded. 
A sample template for executing a CDO is shown in figure 14.7. The code for the buffer described in figure 14.7 is shown in figure 14.8. In creating the ConditionalSend and ConditionalReceive branches, the first argument represents the guard. The second and third arguments represent the port and channel to send or receive the message on. The fourth argument is the identifier assigned to the branch. The choice of placing the guard in the constructor was made to keep the syntax of using guarded communication statements to the minimum, and to have the branch classes resemble the guarded communication statements they represent as closely as possible. This can give rise to the case where the Token specified in a ConditionalSend branch may not yet exist, but this has no effect because once the guard is false, the token in a ConditionalSend is never referenced. 
The other option considered was to wrap the creation of each branch as follows:
if (guard) {
// create branch and place in branches array
} else {
// branches array entry for this branch is null
}
However this leads to longer actor code, and what is happening is not as syntactically obvious.
The code for using a CIF is similar to that in figure 14.7 except that the surrounding while loop is omitted and the case when the identifier returned is -1 does nothing. At some stage the steps involved in using a CIF or a CDO may be automated using a pre-parser, but for now the user must follow the approach described above.
It is worth pointing out that if most channels in a model are buffered, it may be worthwhile considering implementing the model in the PN domain which implicitly has an unbounded buffer on every channel. Also, if modeling time is the principal concern, the model builder should consider using the DE domain.
If a process wishes to use time, the actor representing it must derive from CSPActor. As explained in section 14.2.4, each process in the CSP domain is able to delay itself, either for some period from the current model time or until the next occasion time deadlock is reached at the current model time. The two methods to call are delay() and waitForDeadlock(). Recall that if a process delays itself for zero time from the current time, the process will continue immediately. Thus delay(0.0) is not equivalent to waitForDeadlock()
If no processes are delayed, it is also possible to set the model time by calling the method setCurrentTime() on the director. However, this method can only be called when no processes are delayed, because the state of the model may be rendered meaningless if the model time is advanced to a time beyond the earliest delayed process. This method is present primarily for composing CSP with other domains.
As mentioned in section 14.2.4, as far as each process is concerned, time can only increase while it is blocked waiting to rendezvous or when delaying. A process can be aware of the current model time, but it should only ever affect the model time by delaying its execution, thus forcing time to advance. The method setCurrentTime() should never be called from a process.
By default every model in the CSP domain is timed. To use CSP without a notion of time, do not use the delay() method. The infrastructure supporting time does not affect the model execution if the delay() method is not used.
In a CSP model, the director is an instance of CSPDirector. Since the model is controlled by a CSPDirector, all the receivers in the ports are CSPReceivers. The combination of the CSPDirector and CSPReceivers in the ports gives a model CSP semantics. The CSP domain associates each channel with exactly one receiver, located at the receiving end of the channel. Thus any process that sends or receives to any channel will rendezvous at a CSPReceiver. Figure 14.9 shows the static structure diagram of the five main classes in the CSP kernel, and a few of their associations. These are the classes that provide all the infrastructure needed for a CSP model.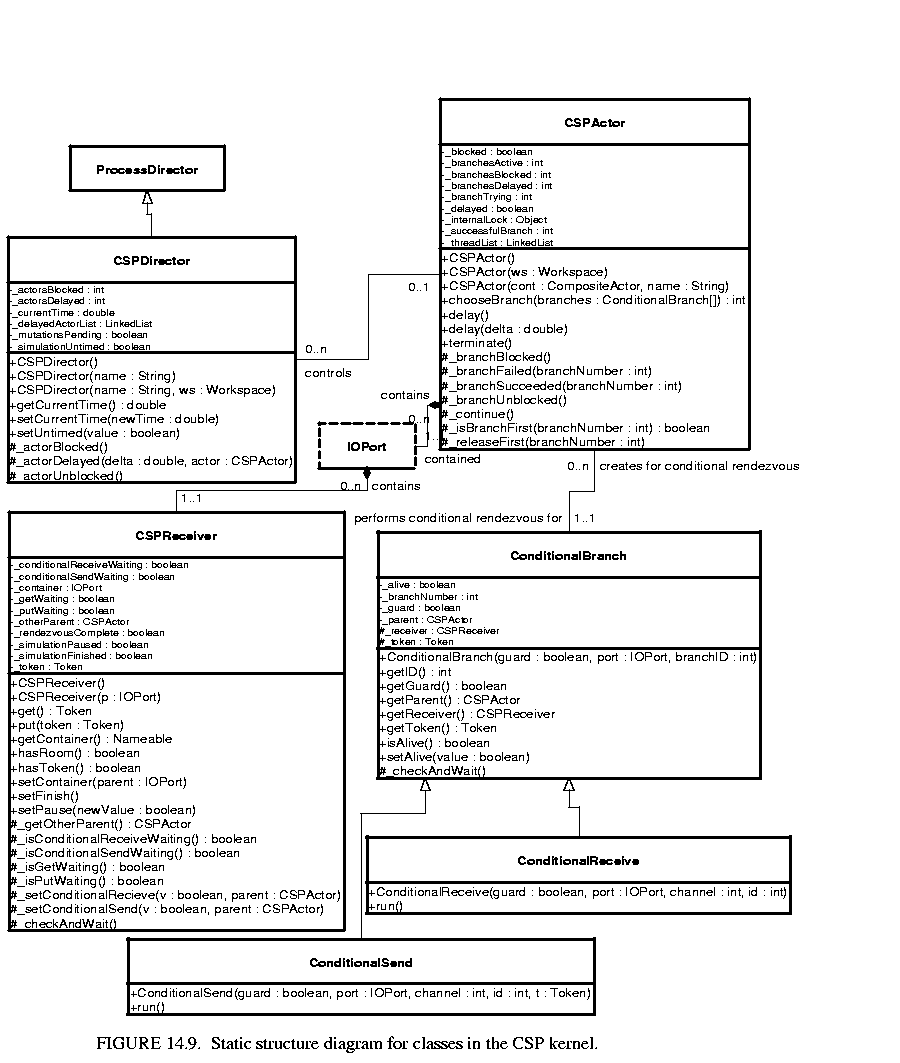 
This gives a model CSP semantics. It takes care of starting all the processes and controls/responds to both real and time deadlocks. It also maintains and advances the model time when necessary.
This ensures that communication of messages between processes is via rendezvous.
This adds the notion of time and the ability to perform conditional communication.
This is used to construct the guarded communication statements necessary for the conditional communication constructs.
The director creates a thread for each actor under its control in its initialize() method. It also invokes the initialize() method on each actor at this time. The director starts the threads in its prefire() method, and detects and responds to deadlocks in its fire() method. The thread for each actor is an instance of ProcessThread, which invokes the prefire(), fire() and postfire() methods for the actor until it finishes or is terminated. It then invokes the wrapup() method and the thread dies.
Figure 14.11 shows the code executed by the ProcessThread class. Note that it makes no assumption about the actor it is executing, so it can execute any domain-polymorphic actor as well as CSP domain-specific actors. In fact, any other domain actor that does not rely on the specifics of its parent domain can be executed in the CSP domain by the ProcessThread.
For deadlock detection, the director maintains three counts:
When the number of blocked processes equals the number of active processes, then real deadlock has occurred and the fire method of the director returns. When the number of blocked plus the number of delayed processes equals the number of active processes, and at least one process is delayed, then time deadlock has occurred. If at least one process is delayed waiting for time deadlock to occur at the current model time, then the director wakes up all such processes and does not advance time. Otherwise the director looks at its list of processes waiting for time to advance, chooses the earliest one and advances time sufficiently to wake it up. It also wakes up any other processes due to be awakened at the new time. The director checks for deadlock each occasion a process blocks, delays or dies.
For the director to work correctly, these three counts need to be accurate at all stages of the model execution, so when they are updated becomes important. Keeping the active count accurate is relatively simple; the director increases it when it starts the thread, and decreases it when the thread dies. Likewise the count of delayed processes is straightforward; when a process delays, it increases the count of delayed processes, and the director keeps track of when to wake it up. The count is decreased when a delayed process resumes.
However, due to the conditional communication constructs, keeping the blocked count accurate requires a little more effort. For a basic send or receive, a process is registered as being blocked when it arrives at the rendezvous point before the matching communication. The blocked count is then decreased by one when the corresponding communication arrives. However what happens when an actor is carrying out a conditional communication construct? In this case the process keeps track of all of the branches for which the guards were true, and when all of those are blocked trying to rendezvous, it registers the process as being blocked. When one of the branches succeeds with a rendezvous, the process is registered as being unblocked.
A process can finish in one of two ways: either by returning false in its prefire() or postfire() methods, in which case it is said to have finished normally, or by being terminated early by a TerminateProcessException. For example, if a source process is intended to send ten tokens and then finish, it would exit its fire() method after sending the tenth token, and return false in its postfire() method. This causes the ProcessThread, see figure 14.11, representing the process, to exit the while loop and execute the finally clause. The finally clause calls wrapup() on the actor it represents, decreases the count of active processes in the director, and the thread representing the process dies.
A TerminateProcessException is thrown whenever a process tries to communicate via a channel whose receiver has its finished flag set to true. When a TerminateProcessException is caught in ProcessThread, the finally clause is also executed and the thread representing the process dies.
To terminate the model, the director sets the finished flag in each receiver. The next occasion a process tries to send to or receive from the channel associated with that receiver, a TerminateProcessException is thrown. This mechanism can also be used in a selective fashion to terminate early any processes that communicate via a particular channel. When the director controlling the execution of the model detects real deadlock, it returns from its fire() method. In the absence of hierarchy, this causes the wrapup() method of the director to be invoked. It is the wrapup() method of the director that sets the finished flag in each receiver. Note that the TerminateProcessException is a runtime exception so it does not need to be declared as being thrown.
There is also the option of abruptly terminating all the processes in the model by calling terminate() on the director. This method differs from the approach described in the previous paragraph in that it stops all the threads immediately and does not give them a chance to update the model state. After calling this method, the state of the model is unknown and so the model should be recreated after calling this method. This method is only intended for situations when the execution of the model has obviously gone wrong, and for it to finish normally would either take too long or could not happen. It should rarely be called.
Pausing and resuming a model does not affect the outcome of a particular execution of the model, only the rate of progress. The execution of a model can be paused at any stage by calling the pause() method on the director. This method is blocking, and will only return when the model execution has been successfully paused. To pause the execution of a model, the director sets a paused flag in every receiver, and the next occasion a process tries to send to or receive from the channel associated with that receiver, it is paused. The whole model is paused when all the active processes are delayed, paused or blocked. To resume the model, the resume() method can similarly be called on the director This method resets the paused flag in every receiver and wakes up every process waiting on a receiver lock. If a process was paused, it sees that it is no longer paused and continues. The ability to pause and resume the execution of a model is intended primarily for user interface control.
The CSP domain, like the rest of Ptolemy II, is written entirely in Java and takes advantage of the features built into the language. In particular, the CSP domain depends heavily on threads and on monitors for controlling the interaction between threads. In any multi-threaded environment, care has to be taken to ensure that the threads do not interact in unintended ways, and that the model does not deadlock. Note deadlock in this sense is a bug in the modeling environment, which is different from the deadlock talked about before which may or may not be a bug in the model being executed.
A monitor is a mechanism for ensuring mutual exclusion between threads. In particular if a thread has a particular monitor, acquired in order to execute some code, then no other thread can simultaneously have that monitor. If another thread tries to acquire that monitor, it stalls until the monitor becomes available. A monitor is also called a lock, and one is associated with every object in Java.
Code that is associated with a lock is defined by the synchronized keyword. This keyword can either be in the signature of a method, in which case the entire method body is associated with that lock, or it can be used in the body of a method using the syntax:
synchronized(object) {
// synchronized code goes here
}
This causes the code inside the brackets to be associated with the lock belonging to the specified object. In either case, when a thread tries to execute code controlled by a lock, it must either acquire the lock or stall until the lock becomes available. If a thread stalls when it already has some locks, those locks are not released, so any other threads waiting on those locks cannot proceed. This can lead to deadlock when all threads are stalled waiting to acquire some lock they need.
A thread can voluntarily relinquish a lock when stalling by calling object.wait() where object is the object to relinquish and wait on. This causes the lock to become available to other threads. A thread can also wake up any threads waiting on a lock associated with an object by calling notifyAll() on the object. Note that to issue a notifyAll() on an object it is necessary to own the lock associated with that object first. By careful use of these methods it is possible to ensure that threads only interact in intended ways and that deadlock does not occur.
One of the key coding patterns followed is to wrap each wait() call in a while loop that checks some flag. Only when the flag is set to false can the thread proceed beyond that point. Thus the code will often look like
synchronized(object) {
...
while(flag) {
object.wait();
}
...
}
The advantage to this is that it is not necessary to worry about what other thread issued the notifyAll() on the lock; the thread can only continue when the notifyAll() is issued and the flag has been set to false.
Another approach used is to keep the number of locks acquired by a thread as few as possible, preferably never more than one at a time. If several threads share the same locks, and they must acquire more than one lock at some stage, then the locks should always be acquired in the same order. To see how this prevent deadlocks, consider two threads, thread1 and thread2, that are using two locks A and B. If thread1 obtains A first, then B, and thread2 obtains B first then A, then a situation could arise whereby thread1 owns lock A and is waiting on B, and thread2 owns lock B and is waiting on A. Neither thread can proceed and so deadlock has occurred. This would be prevented if both threads obtained lock A first, then lock B. This approach is sufficient, but not necessary to prevent deadlocks, as other approaches may also prevent deadlocks without imposing this constraint on the program [43].
Finally, deadlock often occurs even when a thread, which already has some lock, tries to acquire another lock only to issue a notifyAll() on it. To avoid this situation, it is easiest if the notifyAll() is issued from a new thread which has no locks that could be held if it stalls. This is often used in the CSP domain to wake up any threads waiting on receivers, for example after a pause or when terminating the model. The class NotifyThread, in the ptolemy.actor.process package, is used for this purpose. This class takes a list of objects in a linked list, or a single object, and issues a notifyAll() on each of the objects from within a new thread.
The CSP domain kernel makes extensive use of the above patterns and conventions to ensure the modeling engine is deadlock free.
In CSP, the locking point for all communication between processes is the receiver. Any occasion a process wishes to send or receive, it must first acquire the lock for the receiver associated with the channel it is communicating over. Two key facts to keep in mind when reading the following algorithms are that each channel has exactly one receiver associated with it and that at most one process can be trying to send to (or receive from) a channel at any stage. The constraint that each channel can have at most one process trying to send to (or receive from) a channel at any stage is not currently enforced, but an exception will be thrown if such a model is not constructed.
The rendezvous algorithm is entirely symmetric for the put() and the get(), except for the direction the token is transferred. This helps reduce the deadlock situations that could arise and also makes the interaction between processes more understandable and easier to explain. The algorithm controlling how a get() proceeds is shown in figure 14.12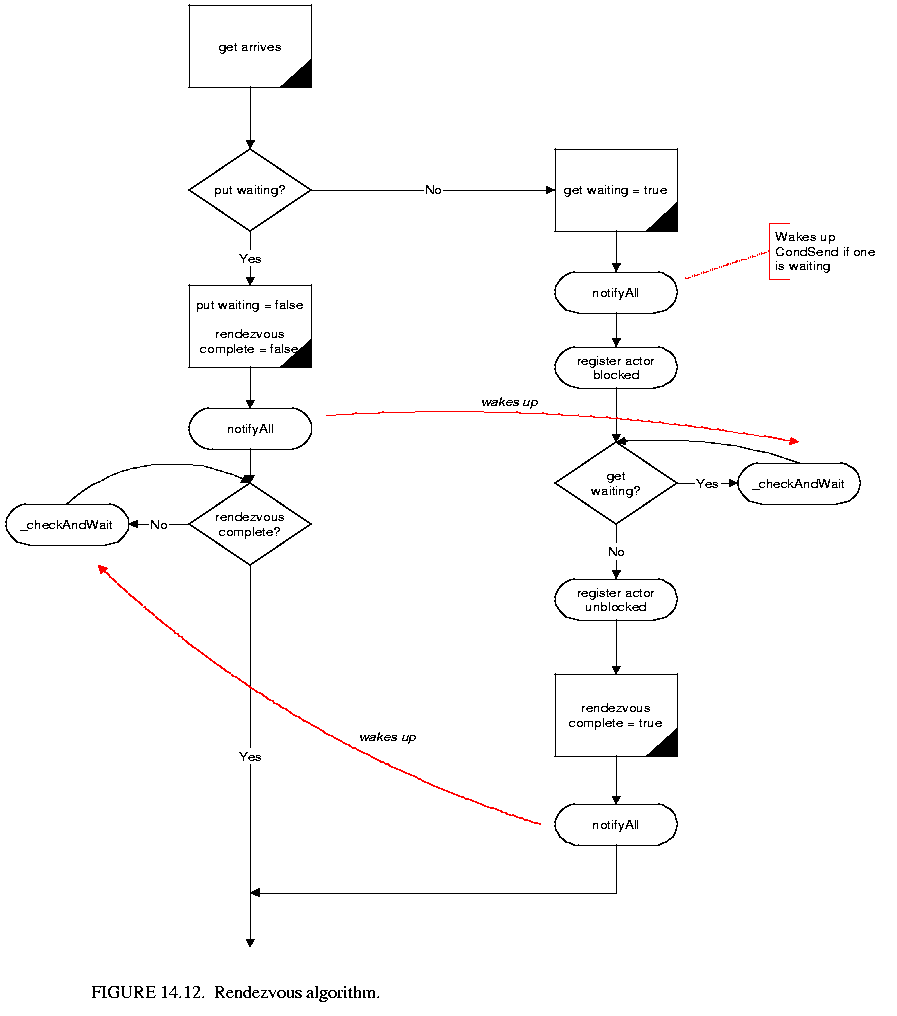
. The algorithm for a put() is exactly the same except that put and get are swapped everywhere. Thus it suffices to explain what happens when a get() arrives at a receiver, i.e. when a process tries to receive from the channel associated with the receiver.
When a get() arrives at a receiver, a put() is either already waiting to rendezvous or it is not. Both the get() and put() methods are entirely synchronized on the receiver so they cannot happen simultaneously (only one thread can possess a lock at any given time). Without loss of generality assume a get() arrives before a put(). The rendezvous mechanism is basically three steps: a get() arrives, a put() arrives, the rendezvous completes.
(1) When the get() arrives, it sees that it is first and sets a flag saying a get is waiting. It then waits on the receiver lock while the flag is still true,
(2) When a put() arrives, it sets the getWaiting flag to false, wakes up any threads waiting on the receiver (including the get), sets the rendezvousComplete flag to false and then waits on the receiver while the rendezvousComplete flag is false,
(3) The thread executing the get() wakes up, sees that a put() has arrived, sets the rendezvousComplete flag to true, wakes up any threads waiting on the receiver and returns thus releasing the lock. The thread executing the put() then wakes up, acquires the receiver lock, sees that the rendezvous is complete and returns.
Following the rendezvous, the state of the receiver is exactly the same as before the rendezvous arrived, and it is ready to mediate another rendezvous. It is worth noting that the final step, of making sure the second communication to arrive does not return until the rendezvous is complete, is necessary to ensure that the correct token gets transferred. Consider the case again when a get() arrives first, except now the put() returns immediately if a get() is already waiting. A put() arrives, places a token in the receiver, sets the get waiting flag to false and returns. Now suppose another put() arrives before the get() wakes up, which will happen if the thread the put() is in wins the race to obtain the lock on the receiver. Then the second put() places a new token in the receiver and sets the put waiting flag to true. Then the get() wakes up, and returns with the wrong token! This is known as a race condition, which will lead to unintended behavior in the model. This situation is avoided by our design.
There are two steps involved in executing a CIF or a CDO: first deciding which enabled branch succeeds, then carrying out the rendezvous.
When a conditional construct has more than one enabled branch (guard is true or absent), a new thread is spawned for each enabled branch. The job of the chooseBranch() method is to control these threads and to determine which branch should be allowed to successfully rendezvous. These threads and the mechanism controlling them are entirely separate from the rendezvous mechanism described in section 14.6.2, with the exception of one special case, which is described in section 14.6.4. Thus the conditional mechanism can be viewed as being built on top of basic rendezvous: conditional communication knows about and needs basic rendezvous, but the opposite is not true. Again this is a design decision which leads to making the interaction between threads easier to understand and is less prone to deadlock as there are fewer interaction possibilities to consider.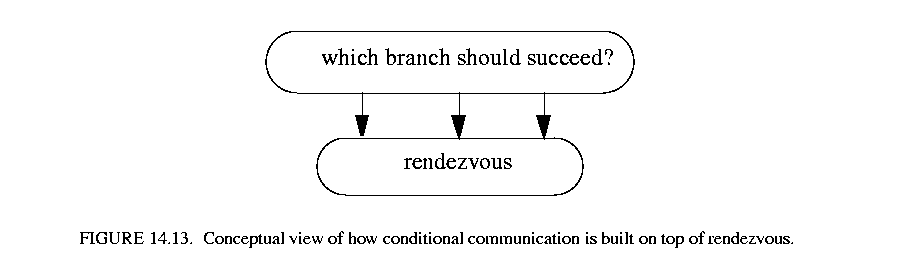
The manner in which the choice of which branch can rendezvous is worth explaining. The chooseBranch() method in CSPActor takes an array of branches as an argument. If all of the guards are false, it returns -1, which indicates that all the branches failed. If exactly one of the guards is true, it performs the rendezvous directly and returns the identification number of the successful branch. The interesting case is when more than one guard is true. In this case, it creates and starts a new thread for each branch whose guard is true. It then waits, on an internal lock, for one branch to succeed. At that point it gets woken up, sets a finished flag in the remaining branches and waits for them to fail. When all the threads representing the branches are finished, it returns the identification number of the successful branch. This approach is designed to ensure that exactly one of the branches created successfully performs a rendezvous.
Similar to the approach followed for rendezvous, the algorithm by which a thread representing a branch determines whether or not it can proceed is entirely symmetrical for a ConditionalSend and a ConditionalReceive. The algorithm followed by a ConditionalReceive is shown figure 14.14. Again the locking point is the receiver, and all code concerned with the communication is synchronized on the receiver. The receiver is also where all necessary flags are stored.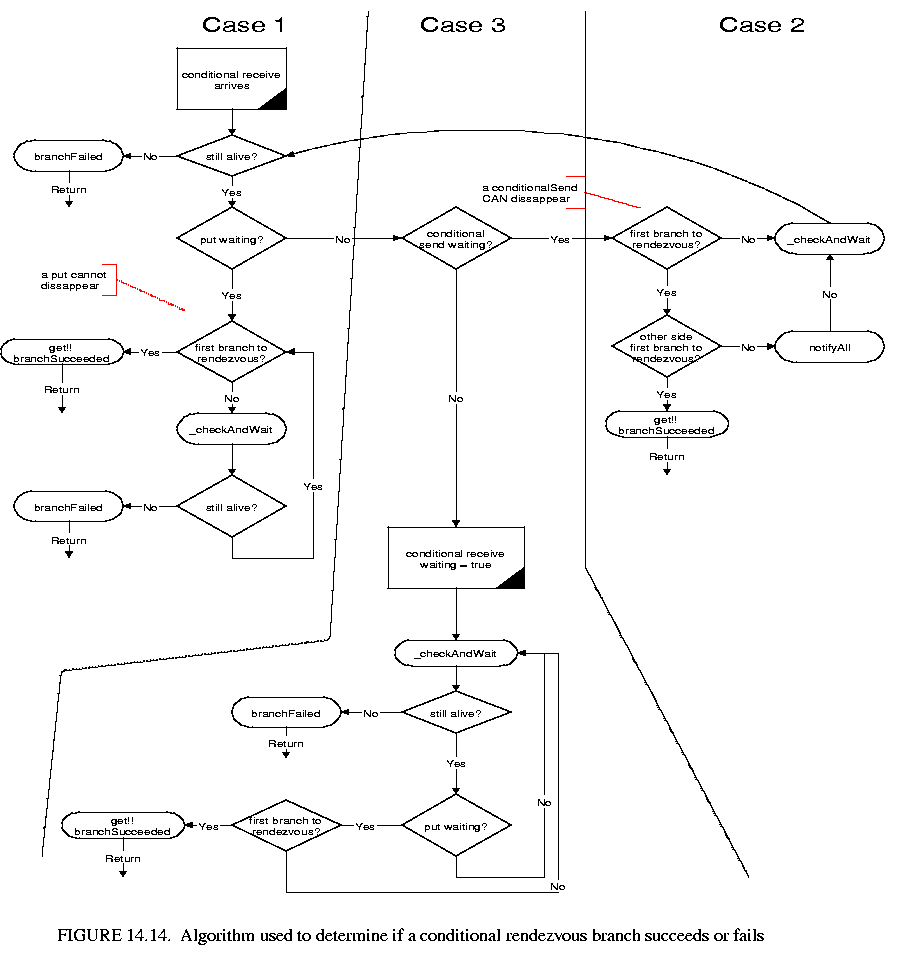
(1) a conditionalReceive arrives and a put is waiting.
In this case, the branch checks if it is the first branch to be ready to rendezvous, and if so, it is goes ahead and executes a get. If it is not the first, it waits on the receiver. When it wakes up, it checks if it is still alive. If it is not, it registers that it has failed and dies. If it is still alive, it starts again by trying to be the first branch to rendezvous. Note that a put cannot disappear.
(2) a conditionalReceive arrives and a conditionalSend is waiting
When both sides are conditional branches, it is up to the branch that arrives second to check whether the rendezvous can proceed. If both branches are the first to try to rendezvous, the conditionalReceive executes a get(), notifies its parent that it succeeded, issues a notifyAll() on the receiver and dies. If not, it checks whether it has been terminated by chooseBranch(). If it has, it registers with chooseBranch() that it has failed and dies. If it has not, it returns to the start of the algorithm and tries again. This is because a ConditionalSend could disappear. Note that the parent of the first branch to arrive at the receiver needs to be stored for the purpose of checking if both branches are the first to arrive.
This part of the algorithm is somewhat subtle. When the second conditional branch arrives at the rendezvous point it checks that both sides are the first to try to rendezvous for their respective processes. If so, then the conditionalReceive executes a get(), so that the conditionalSend is never aware that a conditionalReceive arrived: it only sees the get().
(3) a conditionalReceive arrives first.
It sets a flag in the receiver that it is waiting, then waits on the receiver. When it wakes up, it checks whether it has been killed by chooseBranch. If it has, it registers with chooseBranch that it has failed and dies. Otherwise it checks if a put is waiting. It only needs to check if a put is waiting because if a conditionalSend arrived, it would have behaved as in case (2) above. If a put is waiting, the branch checks if it is the first branch to be ready to rendezvous, and if so it is goes ahead and executes a get. If it is not the first, it waits on the receiver and tries again.
Consider the case when a conditional send arrives before a get. If all the branches in the conditional communication that the conditional send is a part of are blocked, then the process will register itself as blocked with the director. Then the get comes along, and even though a conditional send is waiting, it too would register itself as blocked. This leads to one too many processes being registered as blocked, which could lead to premature deadlock detection.
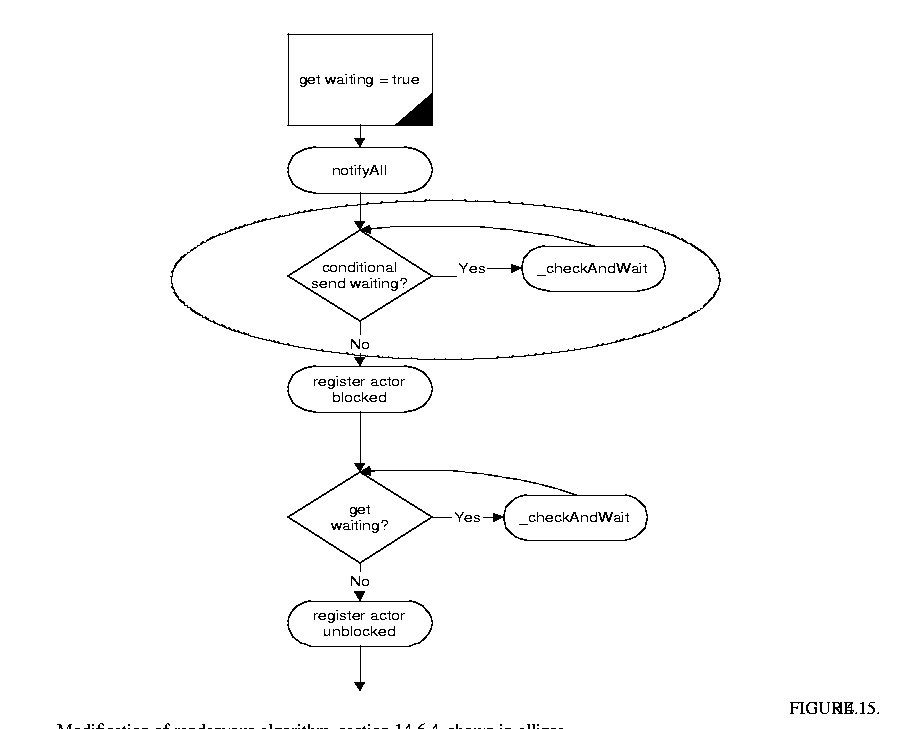
To avoid this, it is necessary to modify the algorithm used for rendezvous slightly. The change to the algorithm is shown in the dashed ellipse in figure 14.15. It does not affect the algorithm except in the case when a conditional send is waiting when a get arrives at the receiver. In this case the process that calls the get should wait on the receiver until the conditional send waiting flag is false. If the conditional send succeeded, and hence executed a put, then the get waiting flag and the conditional send waiting flag should both be false and the actor proceeds through to the third step of the rendezvous. If the conditional send failed, it will have reset the conditional send waiting flag and issued a notifyAll() on the receiver, thus waking up the get and allowing it to properly wait for a put.
The same reasoning also applies to the case when a conditional receive arrives at a receiver before a put.