EECS20N: Signals and Systems

Block diagrams

We have been using block diagrams informally, but now we can define their meaning more formally. A block in a block diagram represents a system, a function on signal spaces. In the picture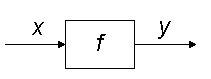

x and y are variables representing signals in some function space, and f is a system that relates these variables by

y = f(x)

The picture

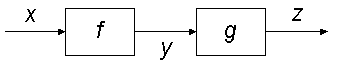
represents the function composition g · f, so that z = g(f (x)). The following picture represents a more complicated form of function composition:

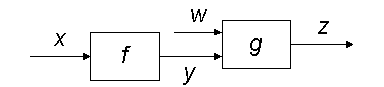
Here, z = g(w, f (x)). A still more complicated block diagram is:

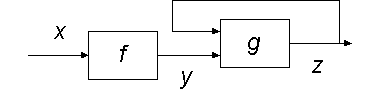
Here, z is defined implicitly as the solution to the equation

z = g(z, f (x)).

Depending on the function spaces and functions involved, this equation may or may not have a solution, and if it has a solution the solution may or may not be unique. Such feedback systems are often powerful solutions to complicated problems.