A Model for Reconstruction
A convenient mathematical model for reconstruction divides the reconstruction process into a cascade of two systems, as shown in the following figure:
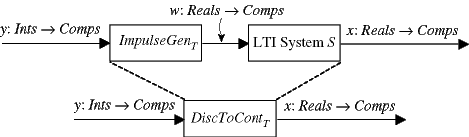
Thus
The first of these two subsystems constructs a continuous-time signal,
where for all t ∈ Reals,
This is a continuous-time signal, albeit an abstract one that would be difficult to construct in the physical world.
The second system is a continuous-time LTI filter, and the impulse response of this filter determines the interpolation method. If
then the interpolation method is zero-order hold. If
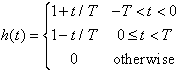
then the interpolation method is linear. If the impulse response is
then the interpolation method is ideal. The above impulse response is called a sinc function, and it is characterized by having no frequency components above π /T radians/sec, the Nyquist frequency. It is this characteristic that makes it ideal.
If we let SincT denote the LTI system H when the impulse response is a sinc function, then
In practice, ideal interpolation is difficult to accomplish. From the expression for the sinc function we can understand why. First, this impulse response is not causal. Second, it is infinite in extent. More importantly, its magnitude decreases rather slowly as t increases (proportional to 1/t only). Thus, truncating it at finite length leads to substantial errors.
This model for reconstruction is illustrated by the following applet:
You can select the interpolation method using the selection box at the upper right. If you select a single sample using the check boxes at the right, you can reconstruct a signal using a subset of the input samples. If you use just one sample, then you see the impulse response of the interpolation system (the LTI system) above. Selecting two neighboring samples, you can see how two neighboring impulse responses combine to interpolate between samples.

 Up to Topics
Up to Topics Previous
Previous Next
Next