Up to Topics
Previous
NextExample of Cascade Composition
Consider the following example, which is a differential precoder cascaded with a decoder.
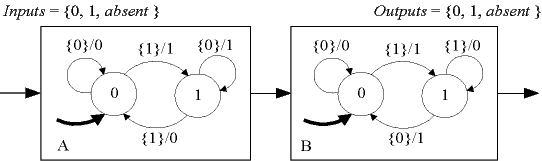
The composition is given by
- States = {(0, 0), (0, 1), (1, 0), (1, 1)}
- Inputs = Outputs = {0, 1, absent }
- initialState = (0, 0)
with update table:
| current state |
(next state, output) for input
|
||
| 0 | 1 | absent | |
| (0, 0) | ((0, 0), 0) | ((1, 1), 1) | ((0, 0), absent) |
| (0, 1) | ((0, 0), 1) | ((1, 1), 0) | ((0, 1), absent) |
| (1, 0) | ((1, 1), 1) | ((0, 0), 0) | ((1, 0), absent) |
| (1, 1) | ((1, 1), 0) | ((0, 0), 1) | ((1, 1), absent) |
Note that states (0, 1) and (1, 0) are not reachable for any input sequence. Furthermore, notice that the output is always equal to the input. This means that the decoder is, in fact, functioning as a decoder. It reverses the effect of the encoder. Can you find a simpler deterministic state machine that is bisimilar to this composition?