Images

A continuous monochrome image is a function

Image: VerticalSpace × HorizontalSpace → Intensity,

where VerticalSpace × HorizontalSpace = [a, b] × [c, d] together represent a region of a plane (the plane in which the image is embedded) and Intensity = [black, white] represents an intensity range from black to white.

For digital images, VerticalSpace, HorizontalSpace, and Intensity must all be discrete, and are usually subsets of Naturals₀, the natural numbers plus zero. A pixel is

Image (row,col) ∈ Intensity, where row ∈ DiscreteVerticalSpace and col ∈ DiscreteHorizontalSpace.

For example, with DiscreteVerticalSpace = {1, 2, ..., 300}, DiscreteHorizontalSpace = {1, 2, ..., 200}, and Intensity = {0, 1, ..., 255}, we get an image is 300 pixels tall by 200 pixels wide, and can have as many as 256 distinct intensities ranging from black to white, as shown below:


300 by 200 pixel image.	Closeup, showing individual pixels.

This particular image is given by a function

Helen: {1, 2, ..., 300}× {1, 2, ..., 200}→ {0, 1, ..., 255}

For any point (x, y) ∈ {1, 2, ..., 300}× {1, 2, ..., 200}, Helen(x, y) gives the gray-scale value of the pixel at point (x, y). The image on the right shows a closeup so that individual pixels can be discerned. The choice Intensity = {0, 1, ..., 255} is convenient because there are 256 elements in this set, and 256 = 2⁸. This means that any element of the set (an intensity) can be represented by an 8 bit binary number.

A color image is a function

Image : DiscreteVerticalSpace × DiscreteHorizontalSpace → Intensity ³,

where now three intensities are given for each pixel. These often represent red, green, and blue (RGB) intensities, respectively, although other formats are also used. Here is an example:


300 by 200 pixel image	closeup, showing individual pixels

The three colors are combined at the display. If each of the RGB colors are given by elements from the set Intensity = {0, 1, ..., 255}, then there are a total of 256 × 256 × 256 = 16,777,216 possible colors. Computer displays can often simultaneously display all of these colors, but it is also common to use a colormap. The widely used CompuServe GIF file format for Internet images uses a colormap.

When a colormap is used, only a subset of the 16 million colors can displayed at any one time in any given image. Typically, the subset has 256 colors in it. The colormap is therefore a table with 256 entries, where each entry consists of three intensities. A color in the table is therefore a member of the set Intensity ³. Each pixel of a color image can then be represented by a single number in the set {1, ..., 256}, the index into the colormap table. Here is a representation of the system that will display the colors:

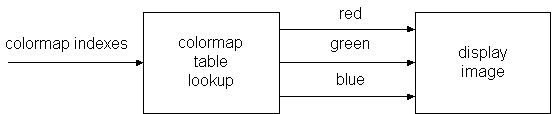
Using such system, an image can be represented by a function

Image : DiscreteVerticalSpace × DiscreteHorizontalSpace → ColormapIndexes,

where ColormapIndexes is the set of indexes into the colormap, typically {1, 2, ..., 256}. The system that displays the image implements the function

Display: ColormapIndexes → Intensity³

Week 1

Images