• Home
•  Up to Topics
•  Previous
•  Next

Week 4

• Nondeterminism
• Example
• Model
• Possible updates
• Relations
• Abstraction
• Equivalence
• Simulation
• Deterministic
• Abstraction
• Nondeterministic
• Behaviors
• Theorem
• Not theorem
• Uses
• Bisimulation
• Examples

Bisimulation

Given two deterministic state machines A and B, if A simulates B, then B simulates A, and A and B are bisimilar. However, for nondeterministc machines, things are much more subtle. In fact, it is possible to have two machines A and B where A simulates B and B simulates A, but A and B are still not bisimilar. Suppose the machines are as follows:

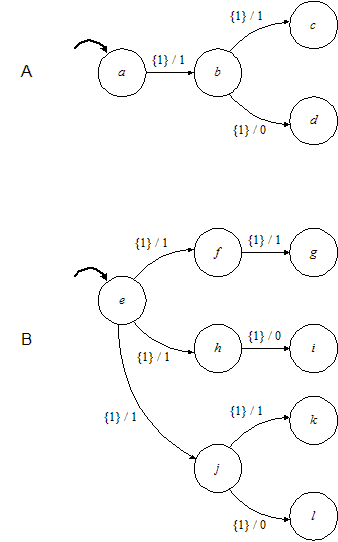
These two machines have exactly the same behaviors. Moreover, A simulates B and B simulates A (we leave this as an exercise for the reader to verify). Nonetheless, these two machines are not bisimilar. To see this, suppose that in that in first round, B moves first, and moves from state e to state f. Then A can match this move by moving to state b. But now, suppose that in round 2, A moves first and moves to state d. In this case, B cannot match this move.

Thus, these two machines are not bisimilar, despite the fact that they have the same behaviors, and they each simulate each other. Bisimulation is truly a strong form of equivalence, much stronger than input/output equivalence, in that it asserts that two machines can match each other's moves even when we flip a coin in each round to determine which machine moves first.