Simulation and Bisimulation
Consider deterministic state machine A:
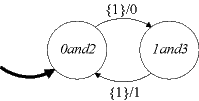
and nondeterministic state machine B:
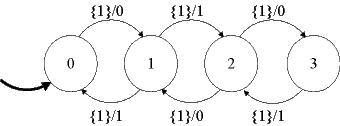
Consider a game, where each machine starts in its initial state. Then, given an input, A reacts, and B tries to react in such a way as to produce the same output (given the same input). For the above examples, B can always do this, so B is said to simulate A. Equivalently, we say that B simulates A.
The game can be turned around, where B makes a move and A tries to match it. In the above examples, this is again possible, so A simulates B. Moreover, in each round of the game, whichever of A or B moves first, the other can match the move. In such circumstances, A and B are said to be bisimilar. Bisimilarity is a strong form of equivalence, stronger than input/output equivalence.
We can track this game by looking at the state responses of the two machines. They each start in their initial state, a fact we can represent with the tuple
( 0and2, 0 ) ∈ StatesA × StatesB
When the first 1 arrives at the input, the two machines change to
( 1and3, 1 ) ∈ StatesA × StatesB
Continuing in this fashion, we see that the states of the two machines are always in the set
{ ( 0and2, 0 ), ( 1and3, 1 ), ( 0and2, 2 ), ( 1and3, 3 ) } ⊂ StatesA × StatesB.
This set is a relation between StatesA and StatesB, and is called the bisimulation relation. Note that the names of the states in machine A are highly suggestive of this relation.

 Up to Topics
Up to Topics Previous
Previous Next
Next